移動する台形が長方形と重なるときの面積 回答
回答
0 ≦ x ≦ 4の時 y=1/2x²
4 ≦ x ≦ 8の時 y=4x – 8
移動する台形が長方形と重なるときの面積 解説
今回の問題は簡単に表すと、
『重なっている部分の底辺の長さx cmと重なっている部分の面積yの関係を式で表しなさい』ということになります。
それでは今回の問題を解いていくにあたって、2つのパターンに分けて考えていきましょう。
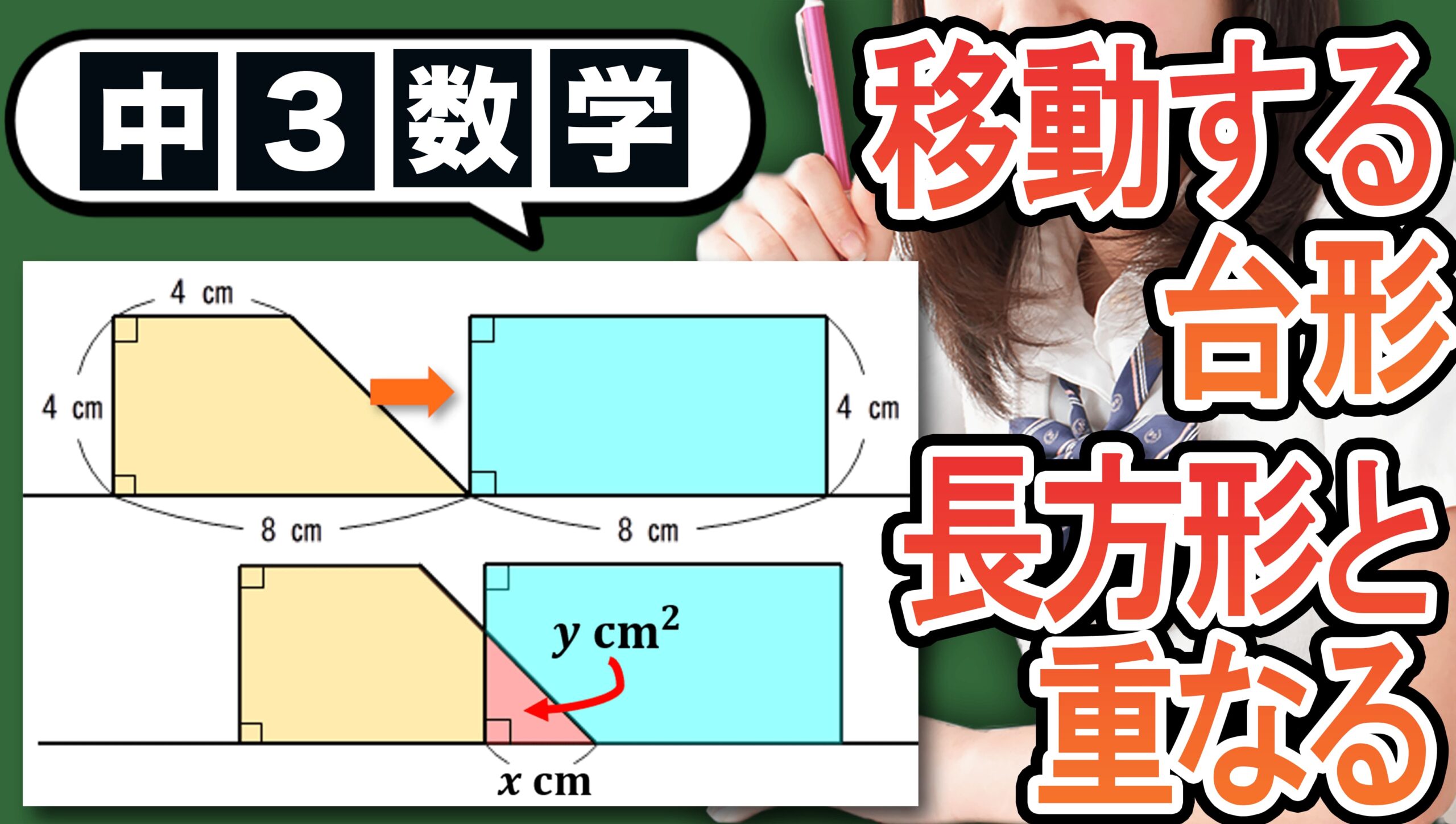
まず①のパターンは、0 ≦ x ≦ 4の時に重なる部分は図の赤い部分です。
直角二等辺三角形になるというのが①のパターンです。
そして②のパターンは、4 ≦ x ≦ 8の時に重なっている部分が図の赤い部分のように台形になります。

①のように台形が移動し始めて最初に重なる部分は直角二等辺三角形になり、直角二等辺三角形の部分が全て重なった時には②のように台形になるということも覚えておきましょう。
①の範囲がなぜ0 ≦ x ≦ 4であるかというと、今回移動する台形の上底の長さは4cmであり、下底の長さは8cmであるということが分かっています。
この上底の右端から垂直に線を引いてあげると、直角二等辺三角形の部分が8 – 4 = 4cmであるということがわかります。
なので、xの範囲が0 ≦ x ≦ 4のとき直角二等辺三角形となり、xの値が4より大きくなったら重なる部分は台形である、ということがわかります。
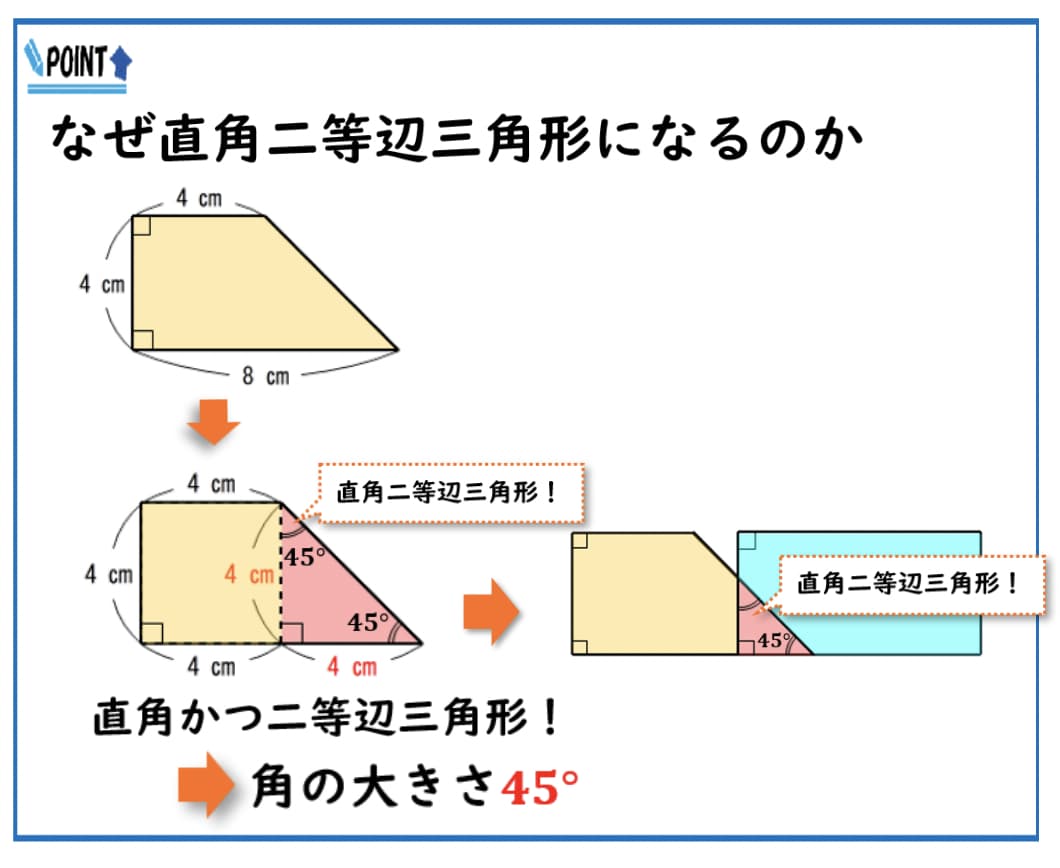
ちなみに、重なっている部分の三角形がなぜ直角三角形になるのか説明しておくと、
今回の台形は高さも4cmであるので、上の図のように台形を正方形と三角形に分けたとき、三角形は直角かつ4cm4cmの二等辺三角形になっているということがわかります。
この台形の右端の角度が45°ということが分かるので重なっている三角形の部分も45°と90°と45°であることが分かるので、こちらも直角二等辺三角形であるということがわかります。
それでは、以上のことを踏まえて①のパターンと②のパターンそれぞれの式を求めていきたいと思います。
①パターン 0 ≦ x ≦ 4 の時の解説

先ほど説明した通り、重なる部分は直角二等辺三角形になるので、底辺がx cmのとき高さもx cmになります。
なので、三角形の面積は『y = 1/2 × x × x』で求めることができます。
※三角形の面積の求め方は『1/2×底辺×高さ』でしたね!
計算をしてあげると、y=1/2x²になり関係式になります。
②パターン 4 ≦ x ≦ 8 の時の解説

②パターンは 4 ≦ x ≦ 8 の時です。
先ほど説明した通り、重なっている部分の形は台形になり、底辺の長さはxcm、高さは4cmです。
台形の面積を求めるにあたって、上底の長さが必要です。
上底の部分の右端から垂線を下ろしてあげると、下底の部分の三角形の部分の長さは4cmであるので、余った部分、x-4cmが上底の長さということがわかります。
台形の面積の公式は『(上底+下底)×高さ×1/2』であるので、
計算
y = {(x – 4) + x} × 4 × 1/2y = (2x -4) × 2
y = 4x – 8
計算をしていくと、y=4x-8であるということがわかりました。
なので
答えは
0 ≦ x ≦ 4の時、y=1/2x²
4 ≦ x ≦ 8の時、y=4x-8
であるということがわかります。
本日のポイント

【1つ目のポイント】
動きをイメージしてパターンを分けましょう!
今回で言うと、最初は直角二等辺三角形でその後が台形になるというのをイメージしましょう。
【2つ目のポイント】
面積を式で表していきましょう!
こちらで移動する台形の関係式は求めることができます。






















コメント一覧