問の回答
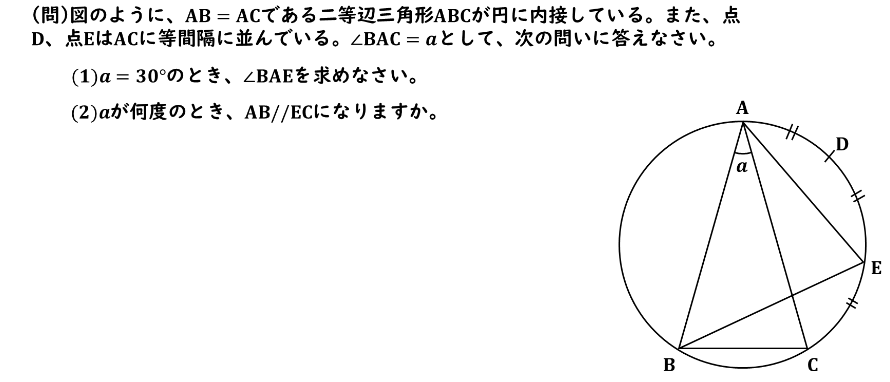
(問) 回答
(1) 55°
(2) 45°
問 (1)の解説
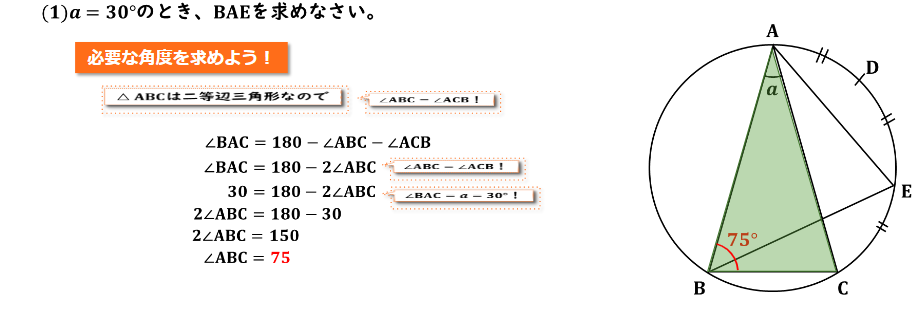
(1) a=30°のとき、∠BAEを求めなさい。の解説をしていきます。
a=30°であるので、この∠EACを含んだ三角形の内角の値を考えていった上で、その周辺の角度の値を徐々に明らかにしていき、最終的に必要な角度である∠BAEの角度を求めていくといった流れになります。ここまでで、なんとなくこの問題を解いていく道筋はつかめたでしょうか。
それでは、まず∠BACが含まれている三角形ABCの内角について考えていきます。ここで問題文で「AB=ACである二等辺三角形」という記載があるため、三角形ABCは二等辺三角形であるということがわかります。つまり底角である∠ABCと∠ACBが等しくなるということが二等辺三角形の性質から言えますね。
三角形の内角の和が180°になることを利用すると、三角形ABCについて、
∠BAC=180°-(∠ABC+∠ACB)
ここで、∠BAC=30°、∠ABC=∠ACBなので上の式は以下のように解けます。
30°=180°-(∠ABC+∠ABC)
↓
2(∠ABC)=150°
↓
∠ABC=75°
よって∠ABC=∠ACB=75°ということが分かりました。
ここからはこの三角形が円に内接していることを利用して、円周角を用いて必要な角度を絞っていきましょう。
まず問題文でも記載されていましたが点Dと点EはACに等間隔に並んでいます。そして円周角の大きさとその円周角に対応する弧の長さはそれぞれ比例の関係にあるため、円周角∠ABEと∠EBCの大きさの比は、それぞれの円周角に対応する弧であるとAEの長さとECの長さの比に等しくなります。
よって∠ABE:∠EBC=AE:ECであるということが言えます。
そして弧AEの長さとECの長さの比は点Dと点Eが等間隔に並んでいることからAE:EC=2:1であるということがわかります。よって
∠ABE:∠EBC=AE:EC
↓
∠ABE:∠EBC=2:1
ことから∠ABEの大きさは、∠ABCに全体の比の大きさである2つの比の値の(1+2)分の2つまり3分の2であるということが言えます。この2/3という値は上の比例式から求めたものであるということは分かるでしょうか。
実際、AE:EC= 2:1のとき、弧ACの長さの比は1と2を足した3になりますよね。つまりAC:AEは3:2となります。そして弧ACから伸びた円周角が∠ABCとなるため
∠ABC:∠ABE=AC:AE
↓
∠ABC:∠ABE=3:2
↓これを解くと(内側×内側=外側×外側なので)
∠ABC:∠ABE=3:2
↓
3(∠ABE)=2(∠ABC)
↓両辺を3で割ると
∠ABE=(2/3)(∠ABC)
となります。
先ほど三角形ABCが二等辺三角形であることから∠ABCの大きさが75°であるということをすでに求めたので、
∠ABE=(2/3)(∠ABC)
↓
∠ABE=(2/3)(75°)
↓
∠ABE=50°となります。
ここで(1)で求めたい角度を改めて整理すると、∠BAEの値を求めるというのが(1)の目的でしたよね。そして今回、∠ABEの大きさを求めることができたので、三角形ABEに着目した時に残りの内角である∠AEBの大きさを求めることができれば、∠BAEの大きさを求めることができるということになります。
そして∠AEBの大きさは、円周角の定理を用いてすぐに求めることが出来ます。今回使う円周角の定理の「1つの弧に対する円周角が等しい」という知識を使います。つまり∠AEBの円周角である弧ABのに注目すると、∠ACBも弧ABの円周角であることがわかります。よって
∠AEB=∠ACBとなります。ここで、∠ACBは75°と求めていたので、∠AEBも75°であるとわかります。

ここで三角ABEに着目すると、∠BAEの大きさは三角形の内角の和である180°から他の2つの内角である∠ABEと∠AEBの大きさを引いた値となります。つまり
∠BAE=180°-(∠ABE+∠AEB)となります。ここで、∠ABE=50°、∠AEB=75°であるので、それぞれ代入して
↓
∠BAE=180°-(50°+75°)
↓
∠BAE=180°-125°
↓
∠BAE=55°
よって(1) a=30°のとき、∠BAEを求めなさい。の答えは55°となります。

問 (2)の解説
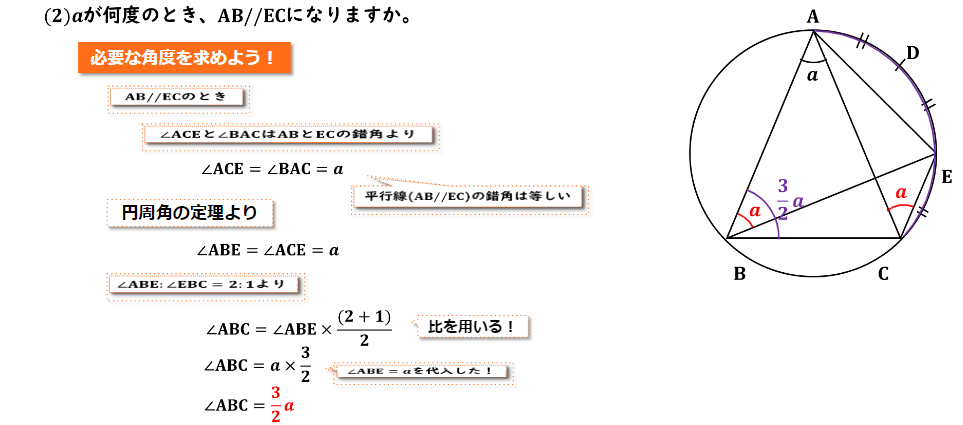
(2) aが何度のとき、AB//ECになりますか。の解説をしていきます。
(2)ではaの具体的な値を問われているということになります。まず(1)と同様に今回の問題で用いることができる図形から必要な角度をそれぞれ整理していきましょう。基本的には三角形が円に内接している時はその円の中 にある三角形の内角の和から角度を求める、といった場合が多いので、今回も円に内接している三角形のどれかから三角形の内角の和が180度であるということを利用するということが予想できます。
そして(2)で特徴的な条件としてABとEC が平行であるということが挙げられます。つまりABとECが平行である時にこの2 つの直線の周辺の角度の関係性がどのように変化するのかといった点に着目していくことが(2)の最大のポイントとなります。
結論から言うと∠ACEと∠BACはABとECの錯角になっていますよね。よって∠ACEと∠BACの大きさは等しいということが言えます。なのでよって∠ACE=∠BAC=aという式が成り立ちます。
(2)はこの直線ABとECが並行であるということから2つの∠ACEと∠EACが平行線の錯角だと気づけるかどうかが最大のポイントでした。2つの平行線というキーワードと必要な角度を求めるというポイントに着目していくと、平行性の錯角という知識を使うのではないかという予想をある程度立てることができます。このように今まで学習してきた知識をどれだけ引き出すことができるか、が図形の問題を得意だと思えるかどうかに関わってくるので、こういった問題がわからなかった時はどの知識を引き出せなかったのか、そしてどのように今まで学習 した知識を使えばよかったのか、を整理した上で自分の頭の中でストックしておくようにしましょう。
そして円周角の定理から弧AEの円周角である∠ACEと∠ABEの大きさが等しいことがわかるため、
∠ACE=∠ABE=aとなります。
そして(1)と同様に、円周角の大きさと弧の大きさが比例の関係にある、ということを利用すると、
∠ABE:∠EBC=AE:EC
↓
∠ABE:∠EBC=2:1
つまり
∠ABC:∠ABE=3:2
↓
3(∠ABE)=2(∠ABC)
↓
∠ABC=(3/2)(∠ABE) これは(1)でも解いているので、ピンとこない場合は戻って確認しましょう。
ここで∠ABE=a°なので∠ABC=(3/2)(∠ABE)に代入して
∠ABC=(3/2)aとなります。
このことから∠ABCが(3/2)aということが分かったので、∠ACBも二等辺三角形の底角であることから(3/2)aであるということがわかります。
よって三角形ABCの内角の和が180度となることを利用すると
∠BAC+∠ABC+∠ACB=180°
↓ここで∠BAC=a、∠ABC=∠ACB=(3/2)aなので代入すると
a+(3/2)a+(3/2)a=180°
↓
4a=180°
↓
a=45°
よって(2) aが何度のとき、AB//ECになりますか。の答えは45°となります。

















関連記事