【相似の利用】縮図 解説動画
本日は中3数学 相似の利用 縮図についてやていきます。
そもそもってなに?
って思いますよね
しかも、参考書の解説がわかりづらくて勉強が嫌になるときありますよね
今回の動画では参考書ではありえないくらい丁寧に解説していきます。
本日の問題はこちらになります。
では解いていきましょう。
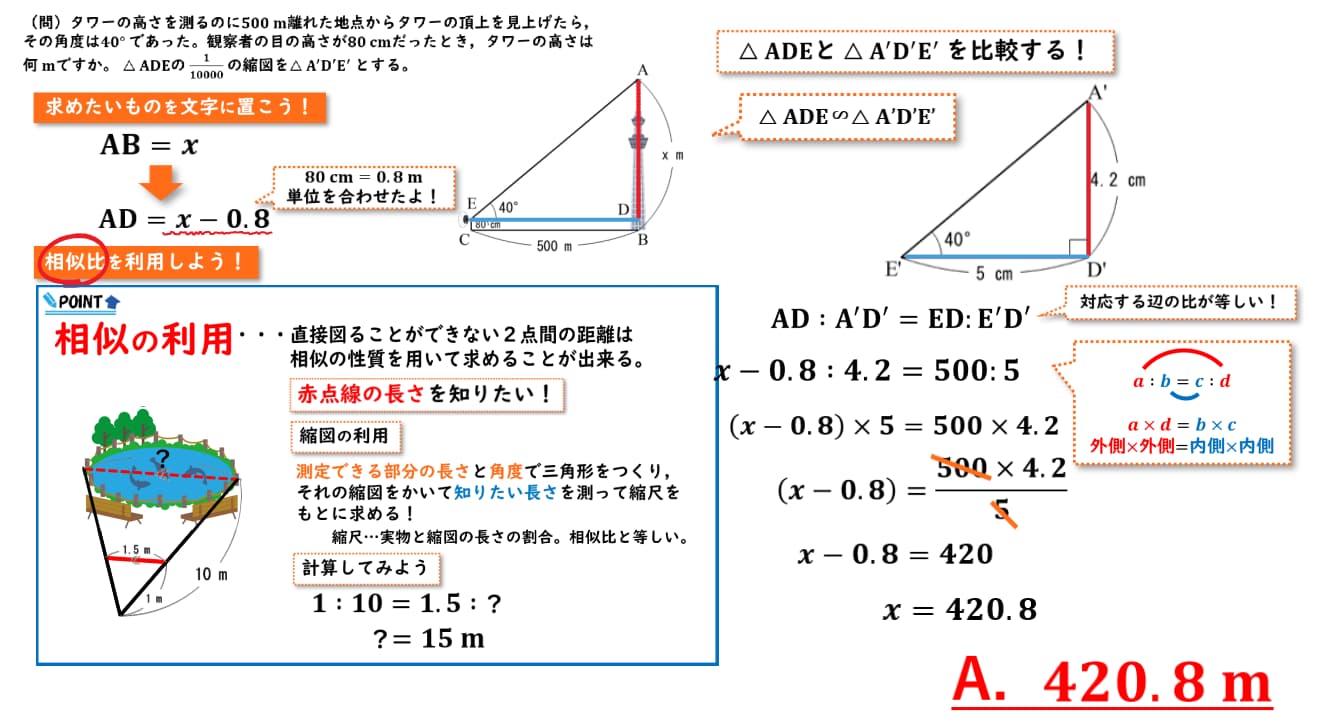
それではまずは、求めたいものを文字としておいてあげましょう。
今回、求めたいのはタワーの高さであり、今回の図で表すとABの長さになります。
なので、ABの長さをxmと書いてあげましょう。
そして今回、三角形をADE活用していきたいので、ADの長さを求めておきたいです。
ADの長さは観察者の目線の高さをタワーの高さから引いてあげればいいので、x – 0.8であることが言えます。
観察者の目の高さは80cmであり、今回は単位を合わせてメートルにすると0.8mと表せます。
それでは相似比も活用していきましょう。
ということで、本日のポイントです。
相似の利用について説明していきたいと思います。
例えば、この池の様に、直接測ることができない2点間の距離は相似の性質を求めることができます。
この図ように赤点線の長さを知りたいと思ったときは縮図を利用してあげましょう。
どのように利用していくかと言うと、測定できる部分の長さと角度で三角形を作ってあげて、それの縮図を書いて知りた
い長さを測って、縮尺を元に求めるというのが縮図の利用になります。
今回で言うと、この図のように小さい三角形と大きい三角形の相似比を活用してきます。
例えば池までの距離が10mである時、1mで縮図を書いてあげました。
この時の赤線の長さは1.5mになるので赤い点線の長さを「?」と置いた時、1 : 10 = 1.5 : ?となります。
こちらの比の計算を解いてあげると、「?」の長さは15mであるという風にわかります。
それでは今回の問題を解きながら説明したいと思います。
それでは三角形ADEと三角形A’B’E’を比較してきましょう。
三角形AB’E’は三角形ADEの縮図であるので、この二つの三角形は相似であるといえます。
相似な三角形の対応する辺の比は、それぞれ等しいのでAD : A’D’ = ED : E’D’になります。
ADの長さはこの赤線の部分。
それに対してA’D’はこの赤線の部分になり、EDの長さはこの青線の部分であり、対応するE’D’はこの青線の部分になりま
す。
それでは、それぞれ分かってる値を代入すると、このようになります。ADの長さは先ほど求めた通り、x = 0.8を代入し
てあげましょう。比の計算は、外側 × 外側 = 内側 × 内側で求めることができるので、( x – 0.8 ) × 5 = 500 × 4.2と
なります。
両辺を5で割ってあげて、計算をするとxの値は420.8であるということが分かりました。
よって今回求めたいタワーの高さは420.8mであるということがわかります。
それでは、本日のポイント
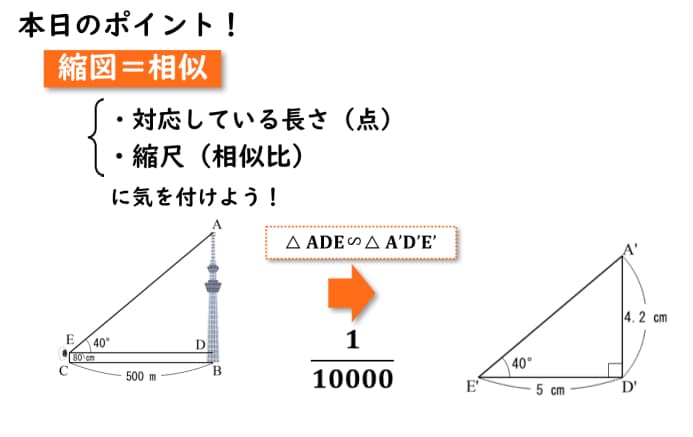
縮図 = 相似と覚えておきましょう。
問題文に縮図と書いてあったら必ず相似を使うという発想をもっておきましょう。
対応している長さと縮尺に気をつけて解いていけば、すんなり解けるかと思います。
本日の授業はいかがでしたでしょうか?
出来た出来ないなどコメントで教えてください。
数学の勉強について悩んでる人向けに公式Lineで質問に答えているので下のボタンから友達追加お願い致します。
Lafの公式LINEで分からない問題が簡単に質問できます!
問題を写真に撮ってチャットで質問できるので解き方が分からない問題があれば気軽に相談してね!
最後まで読んでいただきありがとうございました。


















コメント一覧