平方根について基礎から教えて！
今回は平方根について解説していきます！
平方根とはどのような考え方なのかを押さえることが出来れば、それほど難しい内容ではありません！
今回の内容は、まだ平方根を習っていない方・習ったけれど忘れてしまった方でも理解で切るようにまとめてあります。是非参考にしてください！
因数分解についても知りたい！という方はこちらもチェックしてみてください！
これで完璧！因数分解の基礎の解説完全版！
Laf創業・経営8年目【経歴/実績】
・これまで200名以上のお子様の指導実績あり
国公立をはじめとした難関高への進学をサポート
・AI先生をはじめとした日本初の教育サービスを展開
月間5,000人以上が利用するサービスへと育て上げる
AI先生を利用したことで模試C判定からA判定まで上がったと喜びの声も多数
「話題沸騰中！16大メディアが注目したLaf先生AI – あなたの学びをもっと身近に」
各社が報じた話題のAI教育ツール。24時間質問し放題、理解度に応じた解説で、わからないをゼロに。今すぐ試して、学びを加速させよう。
※様々なメディア様に注目いただき、反響多数！現在TV取材も予定している注目サービスとなっています。（一部掲載）
平方根とは
ここでは、平方根とはどんな考え方をしているのか、
どのように表すのかなどの基本的な内容を扱っていきます。
基礎から見直したいという方はこちらから読み始めてください！
平方根の考え方
平方根とは2乗の逆のことです！
平方根とは2乗の逆のことなので、「2乗したときAになる数がAの平方根である」と言えます。
具体的に数字を当てはめて考えてみましょう。
「2乗したときに36になる数が36の平方根である」
とあったとき、36の平方根は6であることが分かります。
また、-6を2乗しても36になりますね。
そのため、36の平方根は+6と−6になります。6と-6のことをあわせて±6と書くこともあります。
「わかりやすい授業動画」と「練習問題で理解を深めたい方」はコチラ！
＞整数の平方根の求め方！「16の平方根を求めよ」
平方根で使う記号
平方根は根号(ルート)という記号で表されます。
「 √ 」←これをルートと言います。
先ほどの例を記号を使って式にすると
√36=±6
となります。
また、ルートを使うと平方根が整数にならなくても平方根を表すことが出来ます。
例: 「5の平方根」
2乗して5なる数は、本当なら±2.2360…というような数字になります。
しかし、これだと書くのが大変で計算にも不便なので、±√5と書くことが出来ます。
「わかりやすい授業動画」と「練習問題で理解を深めたい方」はコチラ！
＞整数の平方根の求め方！「16の平方根を求めよ」
平方根の正と負
正の数の平方根は、正と負の2つあります。
2乗して負の数になる数は存在しないため、負の数の平方根は存在しません。
よって、ルートの中がマイナスになることは絶対にありません。
√36は36の平方根のうち正の数を表します。つまり、√36 = 6 です。
逆に、-√36は36の平方根のうち負の数を表します。-√36 = -6 です。
0の平方根
平方根は正の数と負の数の二つがあると書きましたが、(A)²= 0 のとき、Aにあてはまるのは0だけとなります。
よって、0の平方根は「0だけ」になります。
0は特別だと覚えておけば、テストで出題されても楽勝で解けますね！
2乗の平方根
2乗の平方根も同じ考え方で解くことが出来ます。
2乗される前の数字が平方根なので、ルートの中で2乗されている数字がその答えになります。
例：
√6² = √36 = 6
-√(7²) = -7
例のように、ルートの外にマイナスがある場合は、答えは負の数になります。
逆に、マイナスがルートの中にある場合、例えば、√(-6)²の倍などは、負の数は2乗されて正の数になりますね！
このパターンの問題は±に気をつけましょう！
「わかりやすい授業動画」と「練習問題で理解を深めたい方」はコチラ！
＞√(-3)²を√を使わないで表す！
■ 平方根の考え方
平方根は2乗の逆！
■ 平方根の記号
√を使って表す
■ 平方根の正と負
正の数の平方根は+と-の二つある
平方根の計算
さて、平方根自体の説明が終わったところで平方根を使った計算方法を解説していきます！
これも基本事項を押さえてしまえば、そんなに難しいことはないので気負わず進んでい行きましょう！
素因数分解を使って数字をまとめる
平方根の計算では、平方根同士の計算ができるよう式を整えます。
式を整えるには素因数分解で数をまとめます。
素因数分解をして2乗で表せる数はルートの外に出します。
これも考えるよりも例題をみて流れを確認していきましょう！
例: √50をまとめる
50の素因数分解は
50 = 2 × 5²
よって、√50 = 5√2
「わかりやすい授業動画」と「練習問題で理解を深めたい方」はコチラ！
＞平方根を a√b に書き換え！～√の中身が整数～
平方根の足し算と引き算
ルートの中身が同じ数字の数は足したり、引いたりすることが出来ます。
逆に、ルートの中身が違う数字の場合、それ以上計算することはできません。
文字式でも同じですよね。
（3a + 4aは7aにまとめられるが、 3a + 4bはこれ以上まとめられない）
つまり、
5√3 + 2√3 = 7√3
とすることが出来ます。
しかし、3√5 + 2√3はこれ以上変わりません。
だから、計算の前に素因数分解が必要になるんですね！
「わかりやすい授業動画」と「練習問題で理解を深めたい方」はコチラ！
＞平方根の足し算!!【中3数学】平方根の計算
足し算・引き算の例題
√27 + √48 – √75 を計算する。
ルートの足し算、または引き算をするため、ルートの中の2乗を外に出して先に数字をまとめます。
√27 = 3√3,
√48 = 4√3,
√75 = 5√3
となり、式は3√3 + 4√3 – 5√3になります。
よって、
√27 + √48 – √75
= 3√3 + 4√3 – 5√3
= 2√3
答えは2√3となります。
平方根の掛け算と割り算
掛け算と割り算では、ルートの中身が違う数字でも計算することができます。
文字式でもそうですね。
例）3a × 4b = 12ab
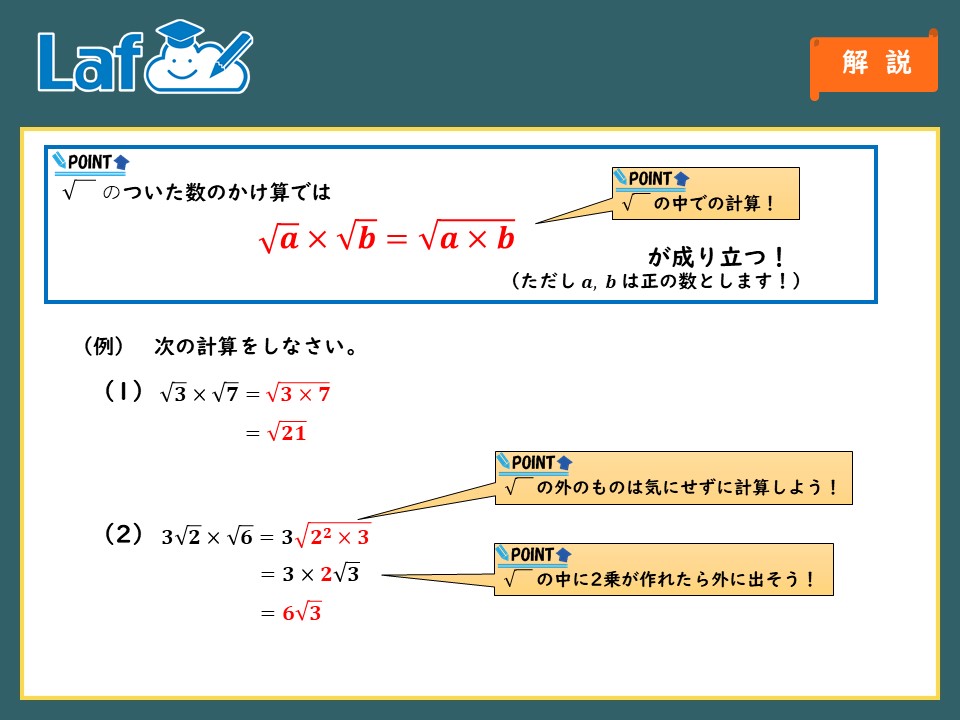
ルートの掛け算はルートの中身同士、ルートの外同士をかけ合わせます。
最後にルートの中から2乗で表せる数字を出して数字を整えます。
例: 3√36 × 4√2を計算する
3√36 × 4√2
= 3 × 4 × √6 × 2
= 12 × √12
= 12 × 2√3
= 24√3
よって答えは24√3となります。
ルートの数字を素因数分解を使ってまとめる癖をつけておきましょう！
「わかりやすい授業動画」と「練習問題で理解を深めたい方」はコチラ！
＞√のついた数のかけ算
分母の有理化
分数を見やすくするため、分母にルートが付いている場合は分母のルートを外して有理化します。
有理化とは「ルートを外すこと」です。難しく考える前に例を見ていきましょう！
例: √28 ÷ √10 を計算する。
先ほどの掛け算と同じ要領で、ルートの中を計算します。
√28/√10 = √14/√5
約分して√14/5になりました。この時点ではルートは分母と分子の両方に掛かっています。
そこで、分母と分子に分母と同じ数を掛けます。
すると、分母だけ2乗されて分母の√が外れます。
√14 × √5 ÷ √5 × √5
= √70 ÷ (√5)²
= √70/5
よって、答えは√70/5となります。
「わかりやすい授業動画」と「練習問題で理解を深めたい方」はコチラ！
＞有理化!!
■ 素因数分解の応用
2乗で表せる数字を√の外に出す
■ 平方根の足し算・引き算
√の中が同じ数字は足し引き出来る
■ 平方根の掛け算・割り算
√の中が違う数字でも掛けたり割ったりできる
■ 分母の有理化
見やすいように分母のルートは外す
覚えておきたい近似値
√4, √9, √16, √25など、平方根が整数になる場合は分かり易いですね。
しかし、√2, √3, √5などは少数点以下が何桁も続く数字になります。
その少数点以下を省略して「だいたいこれくらい」としたのが近似値です。
√2, √3, √5, √7, √8は良く出てきて答えの確認にも使うことが出来るので近似値を覚えておきましょう！
- √2=1.41421356 ひとよひとよにひとみごろ（一夜一夜に人見ごろ）
- √3=1.7320508075 ひとなみにおごれやおなごを（人並みに奢れや女子を)
- √5=2.2360679 ふじさんろくおうむなく（富士山麓オウム鳴く)
- √6=2.44948974 によよくよやくなよ（煮よ 良くよ 焼くなよ）
- √7=2.64575 なにむしいない（菜に虫いない）
- √8=2.8284271 にやにやよにない（ニヤニヤ世担い）
√5の近似値が2.2360679と知っていれば、
「√5000 をルートを使わず小数点第一位まで表しなさい」という問題に即答できます。
2.2360679を1000倍するだけで答えが出ますよね。
また、近似値を覚えておくと現実世界で大体の大きさを測るのに役に立ちます。
√2=1.41421356 一夜一夜に人見ごろ
√3=1.7320508075 人並みに奢れや女子を
√5=2.2360679 富士山麓オウム鳴く
√6=2.44948974 煮よ 良くよ 焼くなよ
√7=2.64575 菜に虫いない
√8=2.8284271 ニヤニヤ世担い
また、近似値の値を活用して解いていく問題については、下の動画をご確認ください！
「わかりやすい授業動画」と「練習問題で理解を深めたい方」はコチラ！
＞√2=1.414の近似値を使って平方根の近似値を求める！【中3数学】平方根
まとめ
いかがでしたでしょうか？
今回は平方根について基礎から解説していきました。
残念ながら、解説を一回読んだだけでは内容は身に付きません。
しっかりと練習問題に取り組み、実力をつけていきましょう！
数学の勉強法について詳しく知りたい方はこちらをチェック！
■ 平方根の考え方を知る
■ √のついた数字をまとめる
■ 平方根の計算方法を知る
■ 分母は有理化する
■ 便利な近似値を覚える
コメント一覧