Laf創業・経営8年目【経歴/実績】
・これまで200名以上のお子様の指導実績あり
国公立をはじめとした難関高への進学をサポート
・AI先生をはじめとした日本初の教育サービスを展開
月間5,000人以上が利用するサービスへと育て上げる
AI先生を利用したことで模試C判定からA判定まで上がったと喜びの声も多数
「話題沸騰中！16大メディアが注目したLaf先生AI – あなたの学びをもっと身近に」
各社が報じた話題のAI教育ツール。24時間質問し放題、理解度に応じた解説で、わからないをゼロに。今すぐ試して、学びを加速させよう。
※様々なメディア様に注目いただき、反響多数！現在TV取材も予定している注目サービスとなっています。（一部掲載）
【二次関数】範囲と料金のグラフ 解説動画
本日は中3数学二次関数 範囲と料金のグラフについてやっていきたいと思います！
範囲と料金のグラフってなに？？って思いますよね。
しかも、参考書の解説がわかりづらくて勉強が嫌になるときありますよね。
今回の動画では、参考書ではありえないくらい丁寧に解説していきますので、チャンネル登録よろしくお願いします！
ちなみに、動画の最後にテスト予想問題を載せているので、チャレンジしてみてください！
それでは二次関数の問題を見ていきましょう！
範囲と料金のグラフの問題
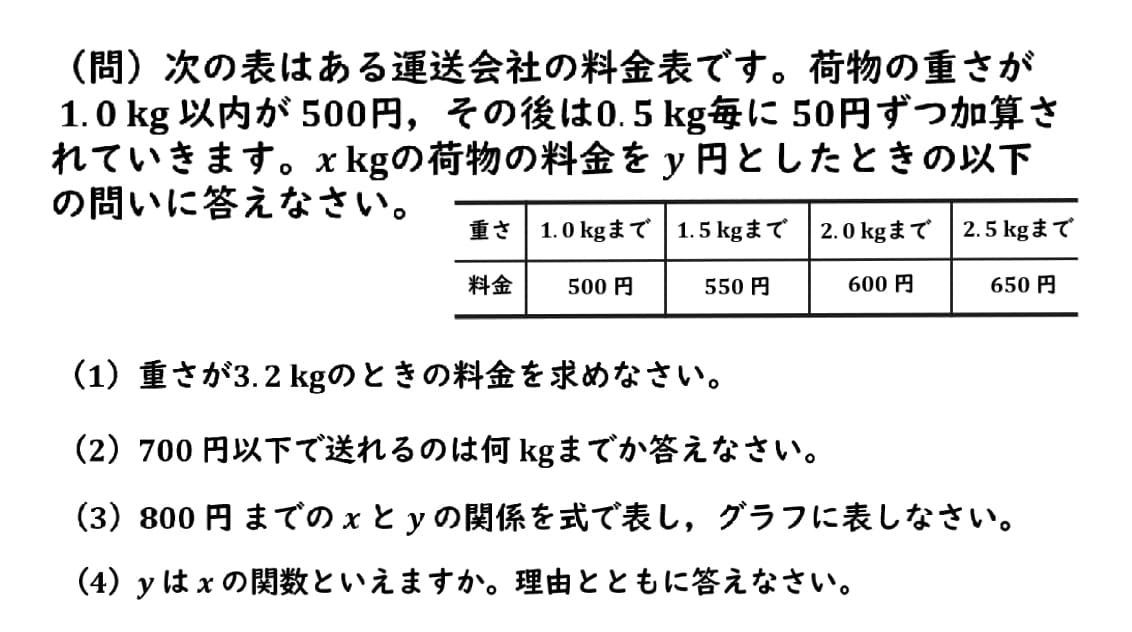
見ていきましょう！
範囲と料金のグラフの解説(1)
まず今回の問題、シンプルに表の右側に条件を書き足していきましょう！
今回の問題文の表はこちらになります。
こちらの表では、2.5kgまでの値しか書いてありません。
なので、勝手に右側に書き加えていきましょう。
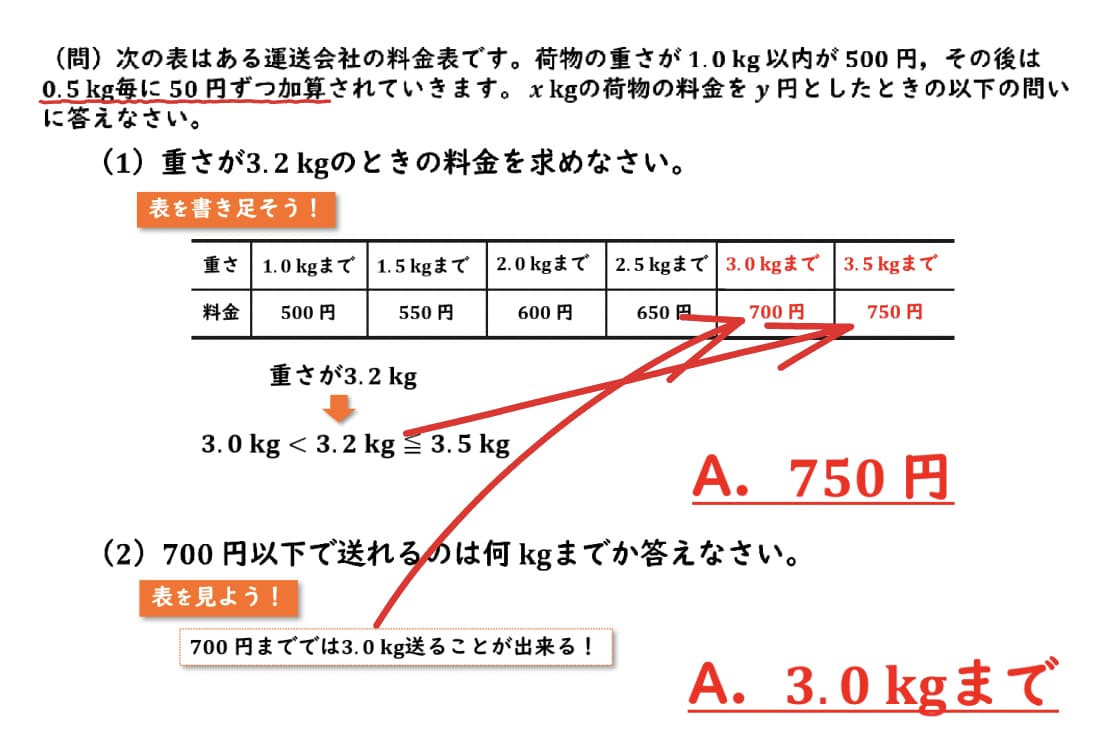
問題文を見ると、0.5kgごとに50円ずつ加算と書いてあるので、2.5kgに0.5kgを足して、3kgまでは700円、3.5kgまでは750円であるということがわかります。
50円ずつ、足し算をしてあげればOKです！
今回求めたい料金は、重さが3.2kgのときなので、3.2kgは3kgより重く、3.5kgより軽いので、表を見てあげると3.5kgまでの料金750円であるということがわかります。
範囲と料金のグラフの解説(2)
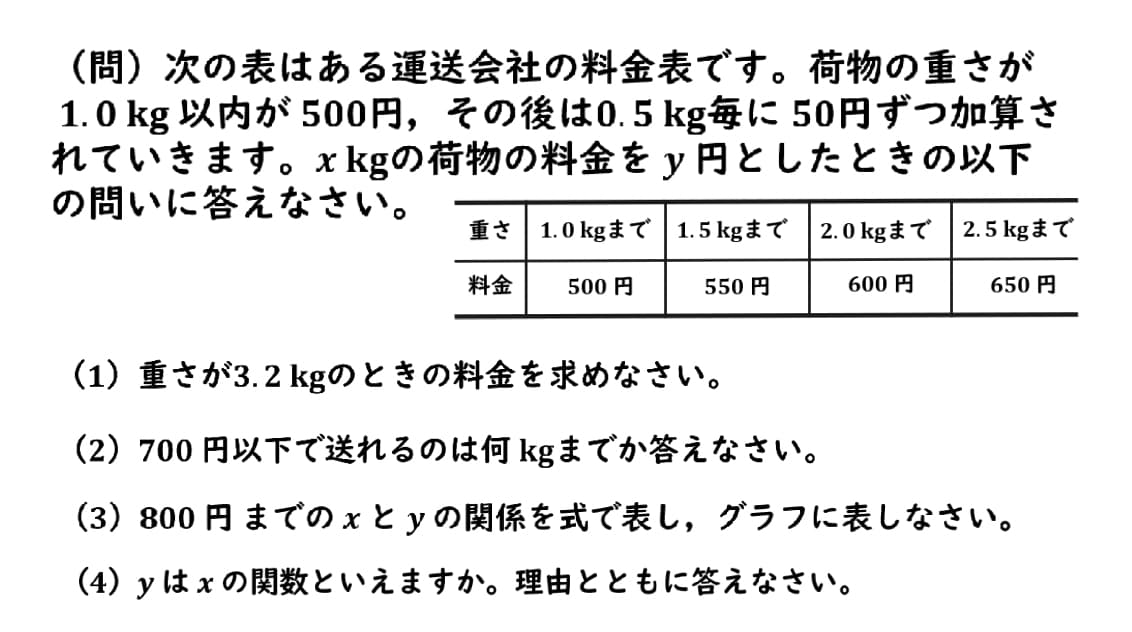
見ていきましょう！
こちらも表を見てあげれば簡単です。
700円までで送ることができるのは3kgなので、答えは3kgまでとなります。
範囲と料金のグラフの解説(3)
見ていきましょう！
まずは、今回の表を改めて書き出してあげましょう。
そして、今回の問題文では、重さをx、料金をyとしたとき、xが1以下は重さが1kgまでということなので、表を見てあげると料金は500円である、すなわち、yの値は500であるということがわかります。
なので、グラフ上にもxが0から1までは、yの値は500であるというのが分かるように書き込んであげましょう。
ちなみに、x=1, y=500の値は赤丸で書いてあげましょう。
赤丸で書くときは、その値を含むということになります。
では次、同様に進めていきましょう。
xが1より大きく1.5以下のとき、表を見てあげると、重さが1.5kgまでなので、料金は550円、yの値は550であるということがわかります。
なので、グラフに書き込んであげるとこのようになります。
このとき、xが1のときは、yの値は500なので、xが1のときのyの値が550のところは白丸で書いてあげ
ましょう。
白丸はその値を含まないということになります。
それでは、この調子で進めていきましょう。
xの値が1.5より大きくて2.0以下のときは、表で確認するとこちらなので、yの値は600、なのでグラフに書いてあげるとこのようになります。
では次、xの値が2より大きくて2.5以下のときは、表に表すとこのようになり、グラフに書き出すとこのようになります。
この調子で、料金が800円すなわちyの値が800を取るまで書き進めると、このようになります。
こちらが、今回のxとyの関係を式で表し、グラフで表したものになります。
本日のポイント
今回のテーマは、色々な関数でした。
今まで習ってきたy=ax+bや、y=ax²のグラフの他にも、yが飛び飛びの値を取ってグラフが階段状になるものもあります。
範囲と料金のグラフの解説(4)
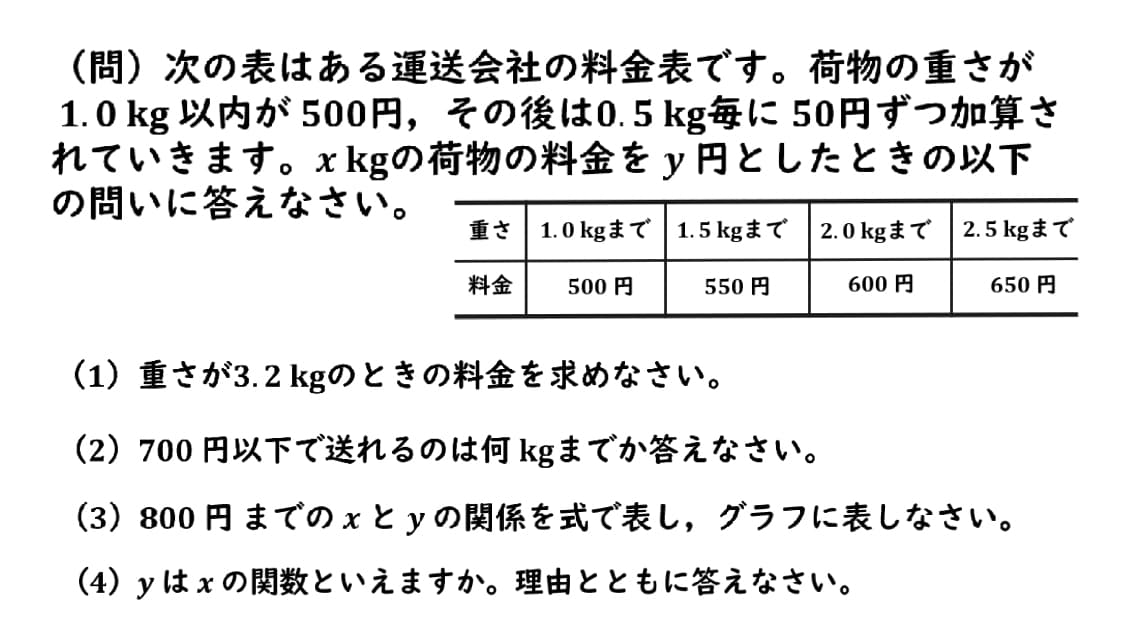
見ていきましょう！
それでは復習！関数とは何か？
関数とは、xとyの関数では、片方の数字が決まれば、もう片方の数字が決まる、というのが関数の関係性でした。
xの値が決まればyの値が決まる、このような関係性を関数と言います。
もっと深く知りたいよ、という方は概要欄の解説動画(1)をチェックしてみてください！
今回のyはxの関数と言えるかどうかですが、答えからお伝えすると、関数と言えます。
理由を説明していくと、今回のグラフはこのようになりました。
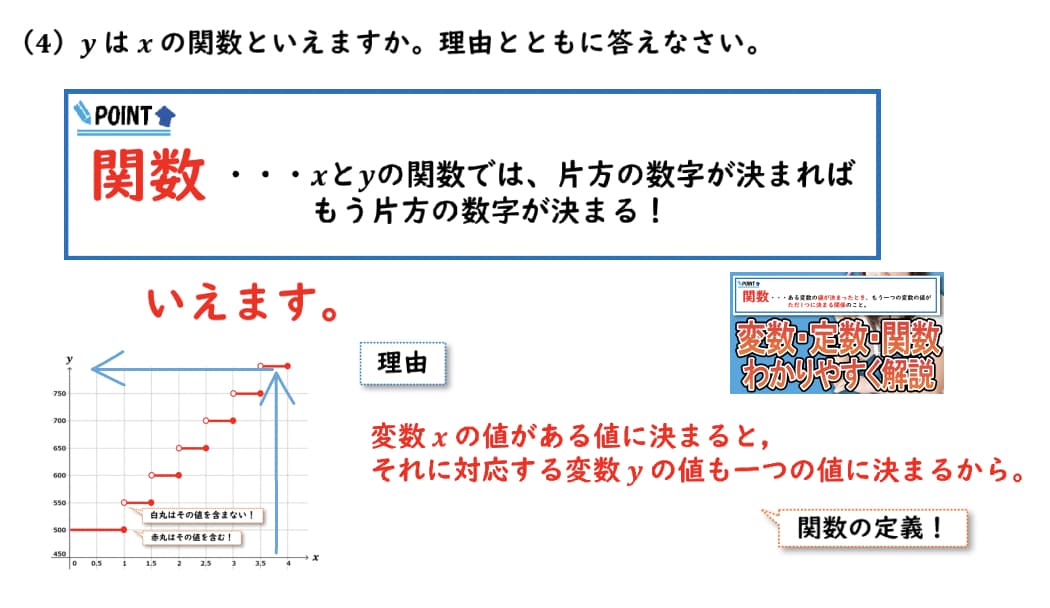
このとき、変数xの値がある方に決まったとき、それに対応する変数yの値も1つの値に決まるから、yはxの関数であると言えます。
こちら、関数の定義そのままですね。
どのxの値をとっても、yの値は一つに決まります。
グラフを見てわかる通り、まずxの値を取って点を見てみると、yの値はただ一つに決まっているというのが分かります。
このような関係性を関数と言います。
ちなみに逆パターンで、yの値が一つに決まったときはxの値は一つに決まらない可能性があるので、逆パターンのxはyの関数であるとは言えないです。
これは補足情報として知っておきましょう！
本日の授業はいかがでしたでしょうか？
出来た！出来ない…！など、是非コメントで教えてください！
数学の勉強について悩んでいる人向けに公式LINEで質問に答えているので、こちらから友達追加お願いいたします！
勉強を頑張っている皆さんがテストで「できる！」ようになるためにテスト予想問題を用意しました！
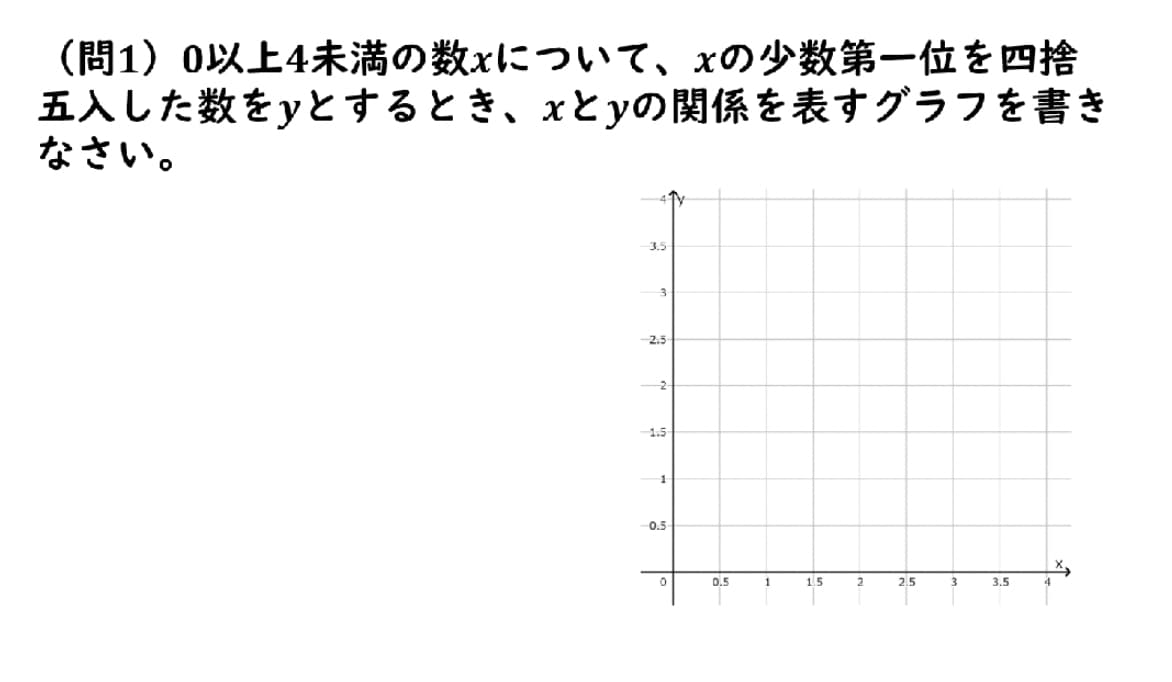
こちらの公式LINEで解説を見ることができるので、チェックしてみてください！
これからも参考書のざっくりとした解説で困らないように、丁寧に解説していきますのでチャンネル登録よろしくお願いいたします！
本日もご視聴ありがとうございました！
コメント一覧