【円】円周角と図形の証明：円周角を用いた円の証明：長さを求めるをわかりやすく解説！【中3数学】

 問の回答

問 (1)の解説

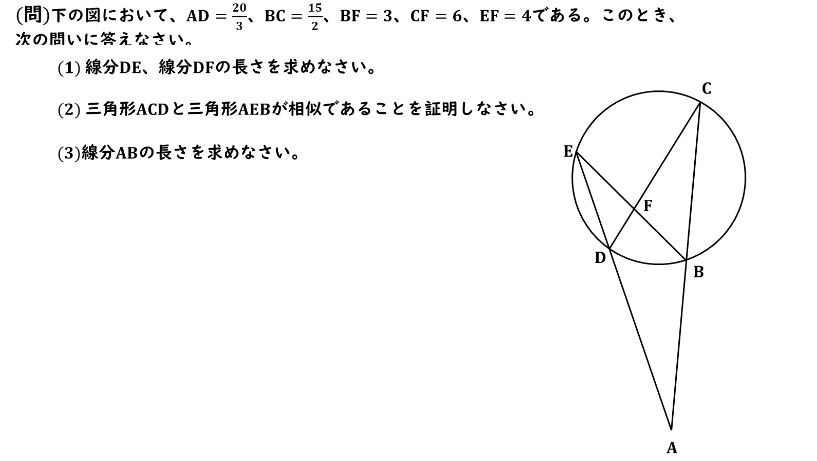
ここでは線DEと線分DFの長さが問われています。この2つの線分の長さを求めていくにあたって、問題文で既に長さが明らかになっている線分がそれぞれ図のどこに記載されているのかをまずは整理していくようにしましょう。

今回はAD=20/3、BC=15/2、BF=3、CF=6、EF=4であるということがわかっています。つまり下の図で青色に塗った三角形BCFの3つの辺の長さはこの時点で全て明らかになっているということがわかりますね。

そしてこの三角形の隣の三角形である三角形DEFに着目していただくと、この三角形は3辺のうち1辺の線分EFの 長さがすでに分かっており、他の2辺の長さが問われている辺となっています。そのためこの2つの三角形が相似であることを証明することができれば、線DEと線分DFの長さを求めることができるということになります。

まず三角形DEFと三角形BCFをそれぞれ見比べると、∠DFEと∠BFCが対頂角であることが分かります。対頂角とは2つの直線が交わる時に向かい合う角のことを言うんでしたよね。そして対頂角は等しいという性質から∠EFEと∠BFCは等しいということが言えます。
よって∠EFE=∠BFC…①

それでは三角形DEFと三角形BCFが相似であることを証明するために、もう一組の等しい角がどれかを見つけていきましょう。ちなみに三角形の相似条件は2組の角がそれぞれ等しいという条件のほかに、3組の辺の比がすべて等しいという条件と、2組の辺の比とその間の角がそれぞれ等しいという条件がありますが、問題で用いられる条件はほとんどが2組の角がそれぞれ等しいという条件になるので、2つの三角形が相似であることを証明したいときはまずは2組の等しい角をそれぞれ見つけていくことを癖付けていきましょう。

そして今回、長さの等しい弧に対応する円周角が等しいという円周角の定理から、∠DEFと∠BCFが等しいということが言えます。
よって∠DEF=∠BCF…②

①と② の条件から三角形DEFと三角形BCFは相似であるということが証明できました。

それではこの2つの三角形が相似であるということが証明できたので、この2つの相似の図形を利用して線DEと線分DFの長さをそれぞれ求めていきましょう。

まず線分DEの長さを求めていきましょう。相似な図形は辺の比が等しいので、
EF:CF=DE:BCという式が成り立ちます。そして線分EFと線分CFそして線分BCの長さはすでに問題文に記載されているため、それぞれの値を代入していくと
4:6=DE:15/2
↓（内側×内側=外側×外側なので）
6DE=30
↓
DE=5
よって線分DEの長さは5であると言えます。

もう一つの線分の長さである線分DFの長さを求めていきましょう。こちらも相似な図形における辺の長さの比を利用して考えていくと、
EF:CF=DF:BCという式が成り立ちます。問題文から線分EF、線分CF、線分BFの長さがそれぞれわかっているので、それぞれ代入していくと
4:6=DF:3
↓
6DF=12
↓
DF=2
よって線分DFの長さは2であると言えます。

問 (2)の解説

(2)は三角形ACDと三角形AEBが相似であることを証明する証明問題となっています。つまり下の図の紫色の三角形ACDとオレンジ色の三角形AEBが相似であることを証明する問題となっています。なおここでも三角形の相似 条件のうち2組の角がそれぞれ等しいという相似条件を使うんだろうな、と思いながら2つの等しい角を探していくようにしましょう。

まずこの2つの三角形を見た時点で∠DACと∠BAEは2つの三角形の共通する角となっていますね。そのため∠DAC=∠BAE…①ということがわかります。

また長さの等しい弧に対応する円周角は等しいという円周角の定理の条件から∠BCF(∠BCD)と∠DEF(∠DEB)はどちらも弧DBに対応する円周角であることから、∠BCF=∠DEFということが言えます。そして∠BCFは∠ACD、∠DEFは∠AEBであるので、∠ACD=∠AEB…②ということがいえます。

①と② の条件から三角形ACDと三角形AEBは相似であるということが証明できました。

ちなみに(2)の証明文の例がこちらになります。ここで証明問題を解いていく際に陥りがちな考え方のミスとして等しい核を見つけられたのに、証明文で書かれている表記の仕方が2つの三角形の辺と結びついていないためすでに2つの角が等しい∠を見つけることができているのに証明文に書くことができないというミスが多く見受けられます。そういった時は照明文を書いている途中でも図に戻って考えるようにしましょう。実際∠BCF=∠DEFと∠ACD=∠AEDはどちらも同じことを言っていますが、その理由は右の図を見ていただくとこの2つの∠はどちらも黒丸で記した2つの角が等しいということを指し示した文章となっていますね。証明問題で行き詰まった時はすぐに図に立ち戻って考える癖をつけるようにしましょう。

問 (3)の解説

(2)でこの2 つの三角形が相似であることを証明したということは(3)でこの2つの三角形の相似比を使えるようにするためということが推測できます。今回の問題のように(1)から(3)まで続いているような問題は(1)や(2)で使った情報が(3)でも使えるというパターンが数学問題では多く見受けられるため、(1)や(2)で得た情報もできるだけ用いて問題を解いていくようにしましょう。

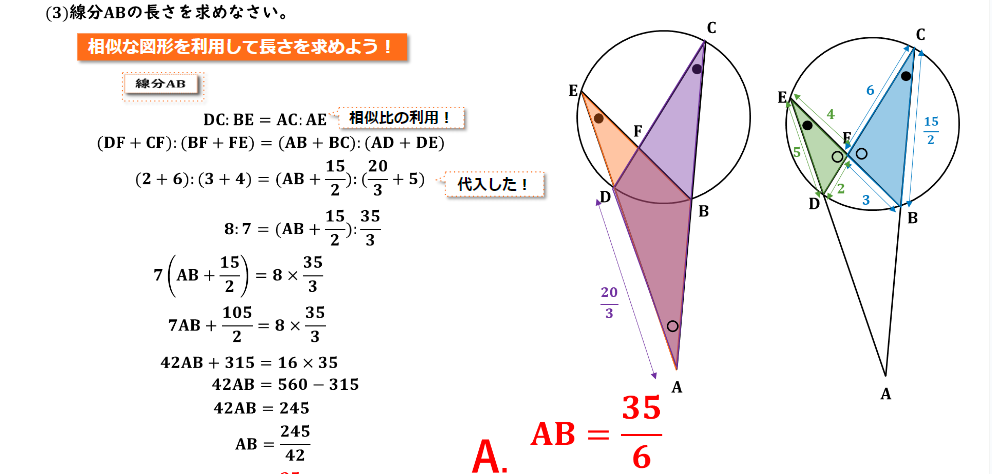
それでは(2)で証明した相似な図形を利用して線分ABの長さを求めていきましょう。

まず相似な図形なので
DC:BE=AC:AEという比例式が成り立ちますよね。

ここで
DC=DF+CF=2+6=8
BE=BF+FE=3+4=7
AC=AB+BC=AB+15/2
AE=AD+DE=20/3+5=35/3
であるので、それぞれの値を代入していくと

8:7=(AB+15/2):35/3
↓（内側×内側=外側×外側なので）
7(AB+15/2)=8×35/3
↓
7AB+105/2=8×35/3
↓（両辺に6をかけて分数をなくすと）
42AB+315=16×35
↓
42AB=560-315
↓
42AB=245
↓
AB=35/6
よって線分ABの長さは35/6であると言えます。