【確率】樹形図!当たりくじをA君とB君が順番に引く問題の解説動画
本日は中2数学確率 樹形図!当たりくじをA君とB君が順番に引く問題について解説していきます。
確率の問題の応用編です!
確率は難しくてわからない、という方も安心してください!
今回は参考書ではありえないくらい丁寧に解説していきます。
成績アップを目指して練習問題に取り組んでみてください。
樹形図!当たりくじをA君とB君が順番に引く問題 練習問題 問1

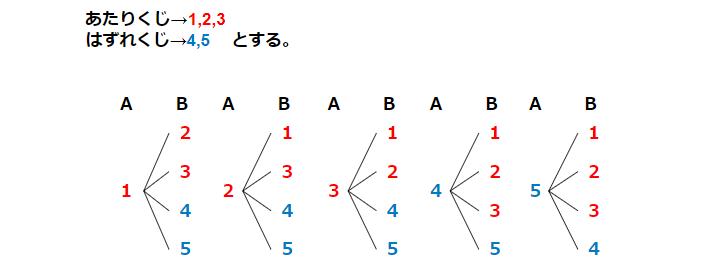
(問1)5本のうち、あたりが3本入っているくじがある。A君、B君の順でくじを引く。ただし引いたくじは元に戻さない、次の問題に答えよ。
(1) 樹形図を書け
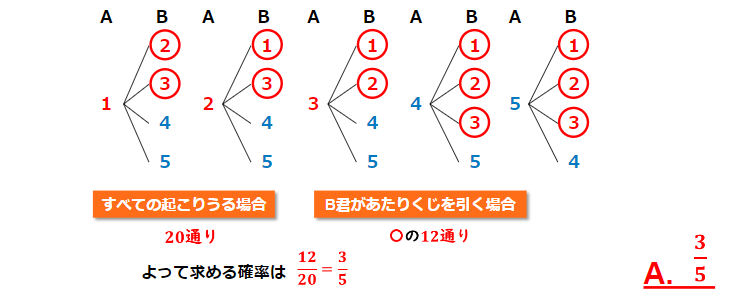
(2) B君があたりくじを引く確率を求めよ
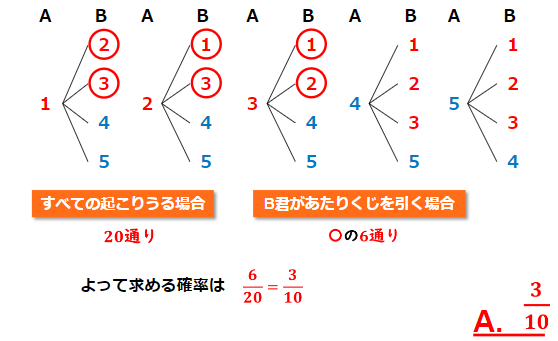
(3) A君、B君ともにあたりくじを引く確率を求めよ
(1) 樹形図を書け
(2) B君があたりくじを引く確率を求めよ
(3) A君、B君ともにあたりくじを引く確率を求めよ
確率の求め方 練習問題 問1 回答と解説
樹形図!当たりくじをA君とB君が順番に引く問題 練習問題 問2

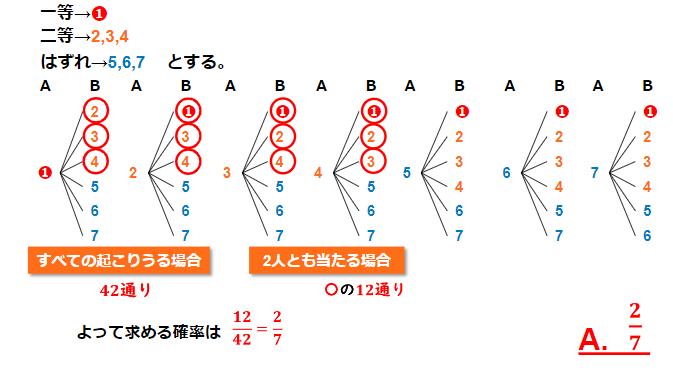
(問2)7本のうち一等が1本、二等が3本入っているくじがある。A,Bの二人がこの順番でくじを引くとき、以下の確率を求めなさい。
(1) 2人とも(二等以上)当たる確率
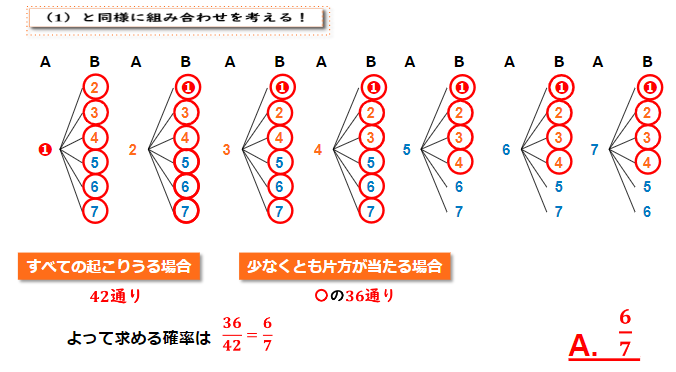
(2) 少なくとも片方が(二等以上)当たる確率
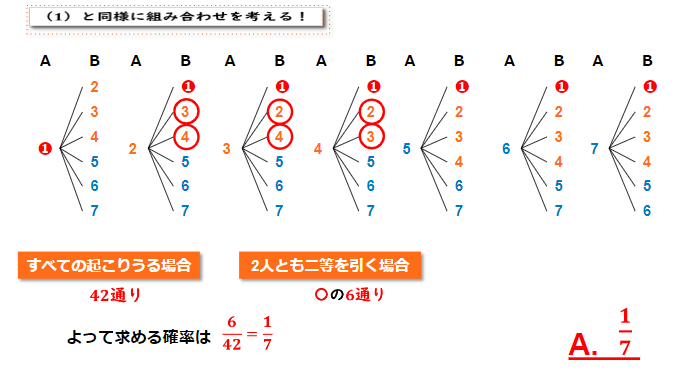
(3) 2人とも二等を引く確率
(1) 2人とも(二等以上)当たる確率
(2) 少なくとも片方が(二等以上)当たる確率
(3) 2人とも二等を引く確率
樹形図!当たりくじをA君とB君が順番に引く問題 練習問題 問2 回答と解説
本日の授業はいかがでしたでしょうか。













関連記事