produce:代表 押川
Laf創業・経営8年目【経歴/実績】
・これまで200名以上のお子様の指導実績あり
国公立をはじめとした難関高への進学をサポート
・AI先生をはじめとした日本初の教育サービスを展開
月間3,000人以上が利用するサービスへと育て上げる
AI先生を利用したことで模試C判定からA判定まで上がったと喜びの声も多数
【学生必見】Zoomで勉強悩み解決!
勉強のお悩み解決します!
(注:Web記事経由限定特典)

- 200人以上の指導をしてきたプロ講師があなたの悩みを親身に聞いて完全解決!
- 3,000人以上の指導実績があるから安心!
- テスト対策、受験勉強、進路相談…なんでもOK!
- カメラオフOK!気軽に相談できるZoom面談!
★★★Web記事からの予約限定特典★★★
- AI先生の全コンテンツを無料で使い放題!
- 志望校別の対策問題集や実力診断テストで学習サポート!
- Zoom相談後もAI先生が継続サポート!
プロのアドバイスとAI先生のサポートで、最短で成績アップ!
お悩み相談で成績が一気にアップした子も
相談枠には限りがあるので、今すぐ公式LINEに登録して、特典をゲットしよう!
勉強悩みを解決して、合格への一直線!
今すぐ予約して、夢への一歩を踏み出そう!
【確率】確率の求め方の解説動画
本日は中2数学確率 確率の求め方について解説していきます。
確率の問題は種類が多くてわからない!と思う人も多いですよね。
参考書の解説もわかりづらくて勉強が嫌になることもあるのではないでしょうか。
今回は参考書ではありえないくらい丁寧に解説していきます。
今回は少し難しいかもしれないので、解き方を考える際のヒントを記載しておきます。
確率の求め方についての学習
問題を解き始める前にまずは確率の求め方を学んでいきましょう。
確率を求めるときは、まずすべての起こり得る場合を考えましょう 。
例えばトランプ52枚の中から1枚だけを取り出す場合を考えてみましょう。
そこで、すべての起こり得る場合とは、ハートの1か、クラブの1か、ダイヤの1か、スペードの1か、ハートの 2か、クラブの2か、、、っていう風に考えていくと 52通りあることがわかりますね。
このすべての場合をn通りとしておきます。
次にこのn通りの中から aが起こる場合の数をa通りで表すと、確率pはn分のaと表すことができます。
例えばトランプで1を取り出せる確率を考えてみましょう。
トランプの1は、ハートの1、クラブの1、ダイヤの1、スペードの1、の4枚あるので、aは4通りとます。
なので トランプ1枚を取り出すとき1である確率は52分の4(=13分の1)ということになりますね。

確率の求め方 練習問題 問1
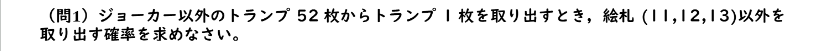
(問1)ジョーカー以外のトランプ52枚からトランプ1枚を取り出すとき、絵札(11,12,13)以外を取り出す確率を求めなさい。
確率の求め方 練習問題 問1 回答と解説
クリックで回答と解説を見る
問1の回答
(問1)回答
10/13
問1の解説
全ての起こり得る場合は52 枚の中から1枚取り出すのでnは52通りありますね。
次に絵札以外は1から10の10通りで、ダイヤ・スペード・クローバー・ハートと4種類あるので、
今回のaは10×4で40通りありますね。
なので今回を求めたい確率は 52分の40となり、約分して13分の10となります。

確率の求め方 練習問題 問2

(問2)次の問いに答えなさい。
(1) さいころを投げるとき、奇数の目が出る確率を求めなさい。
(2) さいころを投げるとき、6以下の目が出る確率を求めなさい。
(3) さいころを投げるとき、7の目が出る確率を求めなさい。
(4) さいころを投げるとき、3の倍数が出る確率を求めなさい。
確率の求め方 練習問題 問2 回答と解説
クリックで回答と解説を見る
問2の回答
(問2) 回答
(1) 2分の1
(2) 1
(3) 0
(4) 3分の1
問2 (1)の解説
サイコロは1から6の6面あるのでnは6通りということになります。
次に奇数の目が出る場合は1、3、5の3つなのでaは3通りとなります。
なので今回を求めたい確率は6通り分の3通りとなり、約分して2分の1となります。
問2 (2)の解説
サイコロを投げるので全ての起こり得る場合nは6通りですね。
6以下の目が出る場合を考えていくと、サイコロの目の1から6すべてが6以下なので、aも6通りとなります。
確率は6分の6となり、約分して確率は1となります。
1ということは 必ず6以下の芽が出るということですね。
問2 (3)の解説
今回も同じようにnは6通りですね。
7の目が出る場合を考えると、サイコロには1から 6の面しかないので7の目はありませんね。なので今回は aは0となります。
それで確率を求めると、6通り分の0通りとなるので、今回の確率は 0が答えとなります。
問2 (4)の解説
今回も同じようにnは6通りですね。
そして3の倍数が出る場合を考えると、サイコロの面の1から6の間で3の倍数は3と6がありますね。なので今回はa=2通りとなります。
それで確率を考えていくと、6通り分の2通りとなるので答えは 3分の1となります。
確率の求め方 練習問題 問3

(問3)袋の中に、赤玉5個、青玉3個、白玉2個が入っています。この中から球を1個取り出すとき、次の確率を求めなさい。
(1) 赤玉出る確率を求めなさい。
(2) 青玉が出る確率を求めなさい。
(3) 青玉または白玉が出る確率を求めなさい。
確率の求め方 練習問題 問3 回答と解説
クリックで回答と解説を見る
問3の回答
(問3) 回答
(1) 2分の1
(2) 10分の3
(3) 2分の1
問3 (1)の解説
今回のすべて起こり得る場合は、赤玉5個、青玉3個、白玉2個入っているので この中から1個取り出す場合nは10通りあることがわかります。
次に、赤玉が出る場合を考えると、赤玉5個入っているのでaは5通りとなります。
なので今回求めたい確率は10通り分の5通りなので、答えは2分の1となります。
すべての起こりうる場合を考えるとき、一見赤玉が出る、青玉が出る、白玉が出る、で3通りと思うかもしれませんが、そうではなく袋の中に何個玉が入っているかで考えていきましょう。 色基準ではなく、個数基準で考える理由としては、赤玉は5個に対して白玉は2個しか入ってませんよね。このように個数に違いがあるので色基準で考えると、とても難しくなってしまいます。なのでまずは何個入っているかを大事にして考えていきましょう。
問3 (2)の解説
今回も同じようにnは10通りですね。
次に、青玉が出る場合を考えると、青玉3個入っているのでaは3通りとなります。
なので今回求めたい確率は10通り分の3通りなので、答えは10分の3となります。
問3 (3)の解説
今回も同じようにnは10通りですね。
そして、青玉または白玉が出る場合なので、青玉が出る場合は3通り、白玉が出る場合は2通りあるので、この3 通りと2通りを足してaは5通りあることがわかります。
なので今回求めたい確率は10通り分の5通りなので、答えは2分の1となります。
確率の求め方 練習問題 問4

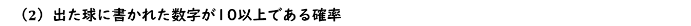
(問4)1,2,3,…,16の数字を1ずつ記入した球を袋の中に入れて、そこから、球を1つ取り出す。このとき、次の確率を求めよ。
(1) 出た球に書かれた数字が4の倍数である確率
(2) 出た球に書かれた数字が10以上である確率
確率の求め方 練習問題 問4 回答と解説
クリックで回答と解説を見る
問4の回答
(問4) 回答
(1) 4分の1
(2) 16分の7
問4 (1)の解説
1から16が書かれた16個の球の中から1つ取り出すので、全ての起こり得る場合nは16通りあることがわかります。
4の倍数である場合は、1から16の間で4、8、12、16の4通りですね。なのでa=4となります。
今回求めたい4の倍数が出る確率は、16通り分の4通りなので、約分すると4分の1が答えとなります。
問4 (2)の解説
今回も同じようにnは16通りですね。
10以上の数字が出る場合は、1から16の間で10、11、12、13、14、15、16の7通りありますね。なのでa=7となります。
今回を求めたい10以上の数字が出る確率は、16 通り分の7通りが答えとなります。
本日の授業はいかがでしたでしょうか。

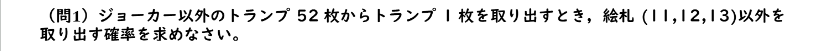



![]()


















関連記事