本日は中3数学 二次関数「一次関数と二次関数の変域が等しい」についてやっていってきたいと思います!
そもそも二次関数の変域が分かりづらいのに、加えて一次関数も出てくるとかもう無理、って思いますよね。
しかも参考書の解説が分かりづらくて勉強が嫌になる時ありますよね。
今回の動画では、参考書ではありえないくらい丁寧に解説していきますのでチャンネル登録よろしくお願いします!
ちなみに、動画の最後にテスト予想問題を載せているのでチャレンジしてみてください!
それでは二次関数の問題見ていきましょう!
本日の問題はこちらになります!

それでは解いていきましょう!
それでは今回、問題文に書いてある通り、yの変域が等しくなると書いてあるので、まずはyの変域を求めていきましょう!
今回の関数は、y=2x+2なので
関数 y=2x+2について、グラフを書きながら考えていきたいと思います。
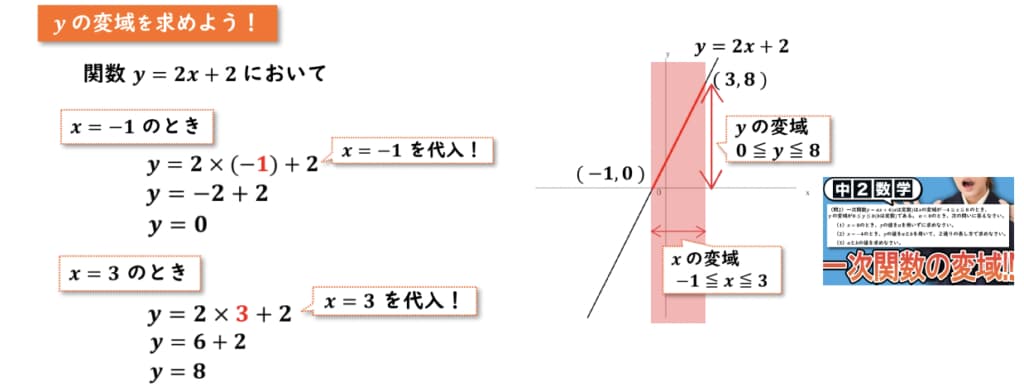
まずグラフを書くとこのようになり、今回、xの変域が-1以上3以下であると書いてあるので、今回のグラフの変域はこの赤線の部分になります!
そうしたとき、yの変域はこの赤矢印の部分になるので、最小値と最大値をそれぞれ求めていきましょう!
まずは、xが-1のときを見ていきましょう。
y-2x+2に、x=-1を代入してあげるとこのようになります。
計算をしてあげると、yが0だということがわかりました!
なので、グラフ上に(-1,0)と書いておいてあげましょう。
では次、x=3のときを考えていきましょう。
こちらも先ほどと同様に、y=2x+2のxの部分に3を代入してあげましょう。
計算をすると、yが8であるということがわかりました。
なのでグラフに最大値としてx=3, y=8を書き込んであげましょう。
よって、今回のyの変域は 0以上8以下 であるということがわかりました!
一次関数の変域についてわからないよ、忘れちゃったよー、という方は、概要欄の解説動画(1)をチェックしてみてください!
それでは、関数y=ax²のaの値を求めていきましょう!
今回の二次関数をグラフで書いてあげると、このようになります。
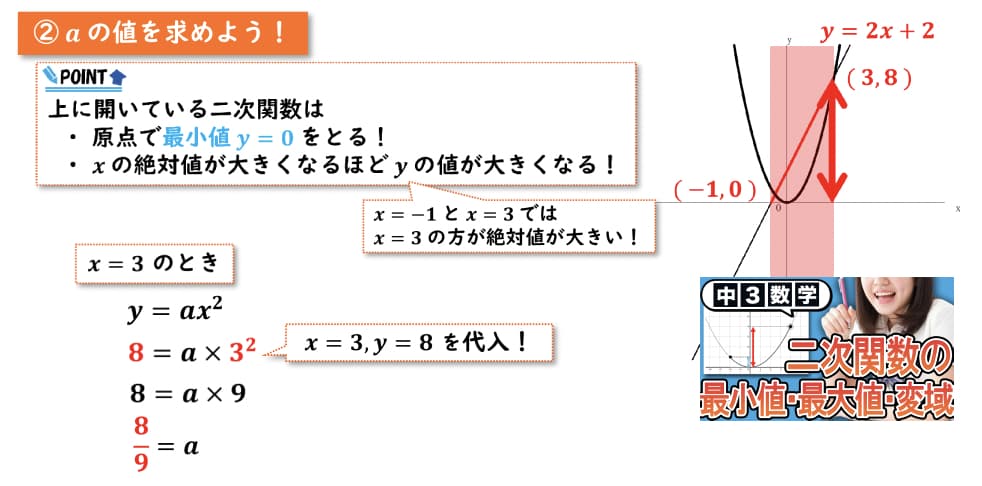
yの変域が 0以上8以下 であるので、二次関数は上に開いている、ということがわかります
それでは本日のポイント!
上に開いている二次関数では、
- 原点で最小値 y=0を取る
- xの絶対値が大きくなるほどyの値が大きくなる
という性質がありました!
この性質がわからないよ、忘れちゃったよー、という方は概要欄の解説動画(2)をチェックしてみてください!
今回のxの変域は -1以上3以下 であるので、
-1と3を比較したときにx=3の方が絶対値が大きいです。
なので、x=3の方が0より離れてる、ということが分かるので
x=3のとき、変域の最大値である8を取る、ということが分かるので
x=3のときを考えていきましょう!
今回の関数 y=ax² のxとyに3と8を代入してあげましょう。
代入すると、このようになります。
計算をしてあげると、aの値は8/9であるということがわかりました!
本日の授業はいかがでしたでしょうか?
できた、できないなどYouTubeのコメントで教えてください!
数学の勉強について悩んでる人向けに公式LINEで質問に答えているので、こちらから友達追加お願いします!

勉強を頑張っている皆さんが、テストでできるようになるために、テスト予想問題を用意しました!
概要欄の公式LINEで解説を見ることができるので、チェックしてみてください!
これからも参考書のざっくりとした解説で困らないように丁寧に解説していきますので、高評価とチャンネル登録よろしくお願いいたします!
本日もありがとうございました!


















コメント一覧