【円】円周角の定理の逆:同一円上の点を求めるの解説動画
本日は中3数学円 円周角の定理の逆:同一円上の点を求めるについて解説していきます。
円の問題は複雑で難しい、と思う人も多いですよね。
参考書の解説もわかりづらくて勉強が嫌になることもあるのではないでしょうか。
今回は参考書ではありえないくらい丁寧に解説していきます。
実際に練習問題を解いて円の問題を練習しましょう。
円周角の定理の逆:同一円上の点を求める 練習問題 問1
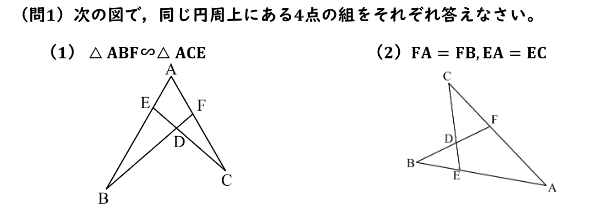
(問1)次の図で、同じ円周上にある4点の組をそれぞれ求めなさい。
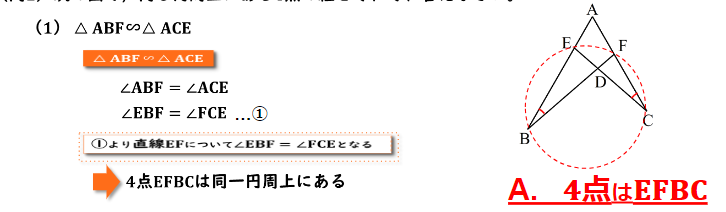
円周角の定理の逆:同一円上の点を求める 練習問題 問1 回答と解説
円周角の定理の逆:同一円上の点を求める 練習問題 問2

(問2)下の図にのように、4点A,B,C,Dは円Oの円周上の点で、線分ADは直径です。2直線AB,CDの交点をE、2直線AC,BDの交点をFとする。このとき、1つの円周上にある4点を答えなさい。
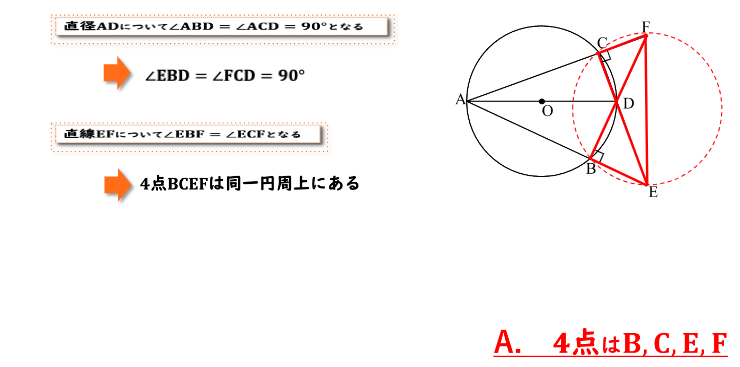
円周角の定理の逆:同一円上の点を求める 練習問題 問2 回答と解説
本日の授業はいかがでしたでしょうか。














関連記事