【確率】弧と中心角と円周角:弧の比から長さと角度を求めるの解説動画
本日は中3数学円 弧と中心角と円周角:弧の比から長さと角度を求めるについて解説していきます。
円の問題は複雑で難しい、と思う人も多いですよね。
参考書の解説もわかりづらくて勉強が嫌になることもあるのではないでしょうか。
今回は参考書ではありえないくらい丁寧に解説していきます。
前半では弧と中心角、弧と円周角の関係について学習しましょう。
後半では実際に練習問題を解いて円の問題を練習しましょう。
弧と中心角、円周角について学習
弧と中心角の関係
①弧の長さが等しいとき、中心角の大きさも等しい。
②中心角の大きさが等しいとき、弧の長さも等しい。
同一円において、弧の長さと中心角の大きさは比例の関係にある。

弧と円周角の関係
①弧の長さが等しいとき、円周角の大きさも等しい。
②円周角の大きさが等しいとき、弧の長さも等しい。
同一円において、弧の長さと円周角の大きさは比例の関係にある。

弧と中心角と円周角:弧の比から長さと角度を求める 練習問題 問1

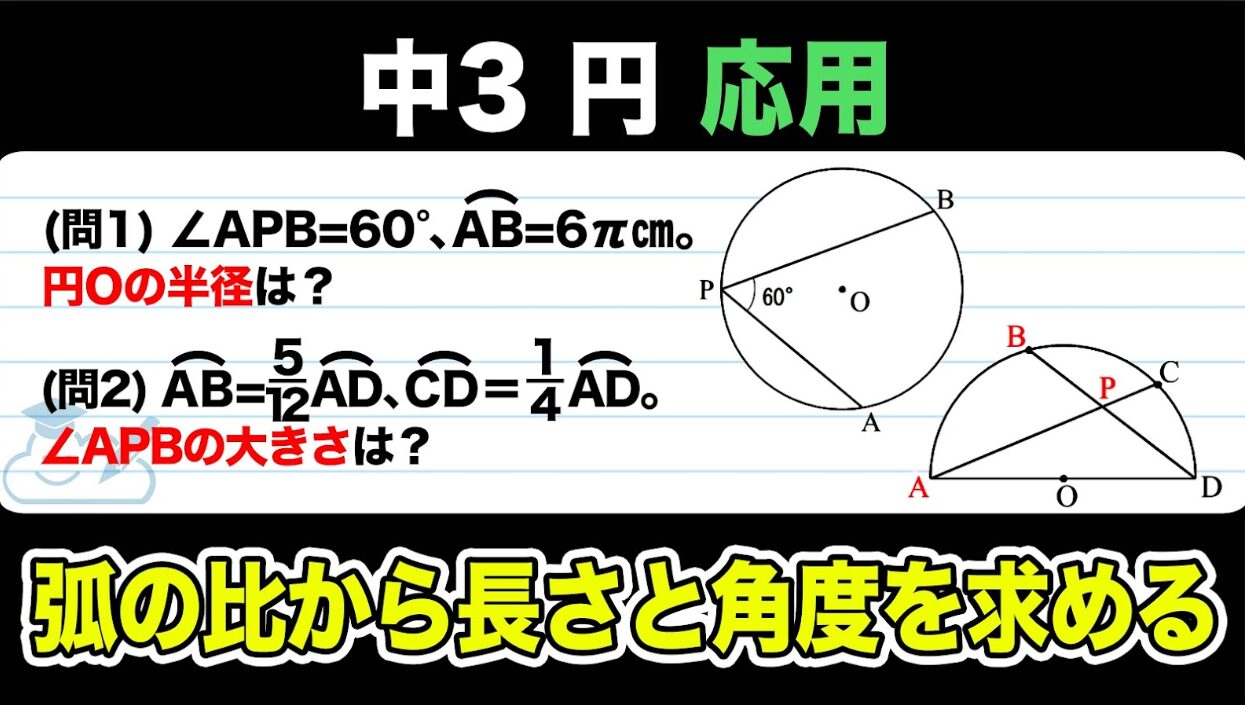
(問1)右の円Oにおいて、弧ABの円周角を∠APB=60°、弧AB=6π cmであるとき、円Oの半径を求めなさい。
弧と中心角と円周角:弧の比から長さと角度を求める 問1 回答と解説
クリックで回答と解説を見る
問1の回答
(問1) 回答
9 cm
問1の解説
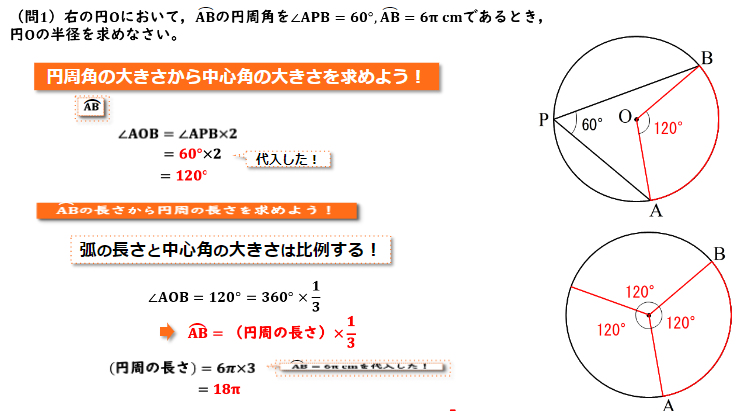
問題から、長さ6πの弧ABに対する円周角は60度であることが分かっています
この円周角から中心角を求めていきましょう。
中心角は円周角の2倍となるので、弧ABに対する中心角は120度であることがわかります。
中心角がわかったのでそこから円周の長さを求めていきましょう。弧の長さと中心角の大きさは比例する、ということを利用します。
中心角120度に対して弧ABが6πであることがわかっています。円周は中心角360度に対する弧の長さとも考えられるので、弧ABは演習の長さの1/3倍であることがわかります。
よって円周の長さは弧ABの長さ6πの3倍、つまり18πとなります。
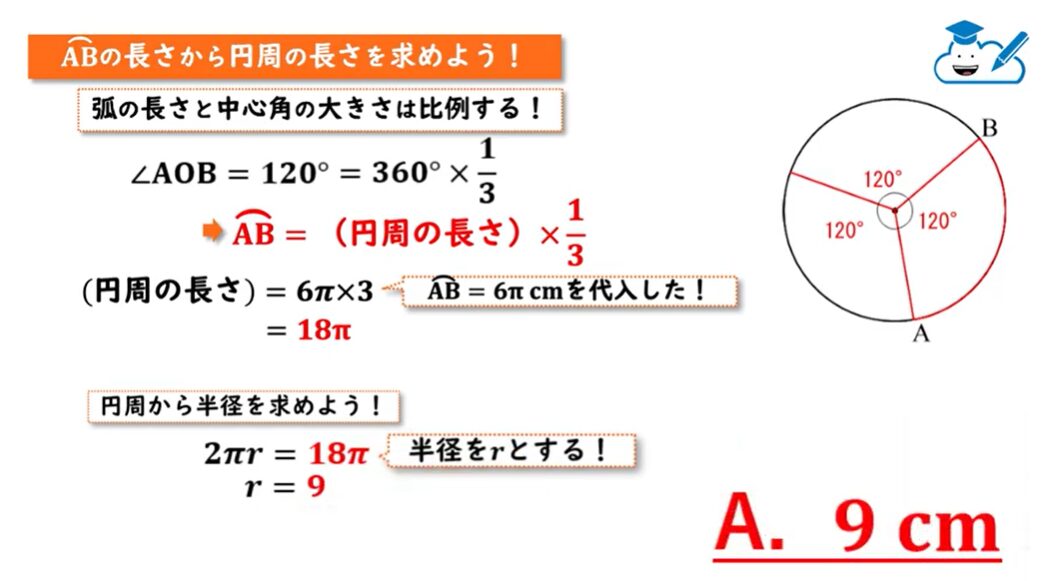
円周の長さがわかったら、そこから半径を求めていきましょう。
半径の長さをrとすると2πrが演習となります。
なのでrについて解いてあげると、問1の答えは9cmとなります。
弧と中心角と円周角:弧の比から長さと角度を求める 練習問題 問2

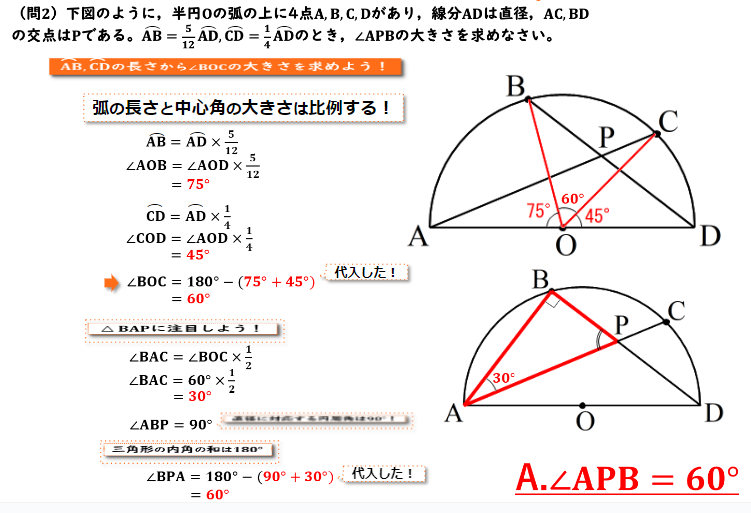
(問2)図のように、半円Oの弧の上に4点A,B,C,Dがあり、線分ADは直径、AC,BDの交点はPである。弧AB=(5/12)弧AD、弧CD=(1/4)弧ADのとき、∠APBの大きさを求めなさい。
弧と中心角と円周角:弧の比から長さと角度を求める 問2 回答と解説
クリックで回答と解説を見る
問2の回答
(問2) 回答
60°
問2の解説
∠APBの大きさを求められているので、三角形BAPに注目していきましょう。
三角形BAPに注目すると、直径に対応する円周角が90度であるので、∠ABPは90度であることがわかります。
∠ABPの大きさがわかったので、次に∠BAPの大きさが分かれば、∠APBの大きさを求められそうですね。
ですが、まずは∠BAPを∠BAC、つまり弧BCに対する円周角として求めていきましょう。
∠BAPは弧BCの円周角なので、∠BCの中心角が分かれば求めることができます。
∠ABと∠CDの長さから∠BOC、つまり弧BCに対する中心角の大きさを求めていきましょう。
まず弧ABに注目すると、問題より、弧ABは弧ADの12分の5倍でした。つまり弧ABに対する中心角∠AOBは弧ADに対する中心角∠AODの12分の5倍であることがわかります。ここで問題文から ADは直径であることがわかっているので∠AODは180度であることがわかります。なので∠AOBの大きさは180に12分の5をかけた75度ということになります。
同じように弧CDは弧ADの4分の1倍、つまり180度の4分の1倍となるので45度と計算できます。
したがって∠BOCの大きさは180-(75+45)と計算でき、60度であることがわかりました。
弧BCに対する中心角が計算できたので∠BAPを求めていきましょう。
∠BAPつまり弧BCに対する円周角∠PACは弧BCに対する中心角POCの1/2倍であることがわかるので、60度の1/2倍つまり30度であることが計算できます。なので∠BAPは30度であることが分かりました。
最後に今回問われている∠BPAは180度から∠ABPと∠BAPを引いた値となるので、∠BPAは60度となります。
弧と中心角と円周角:弧の比から長さと角度を求める 練習問題 問3

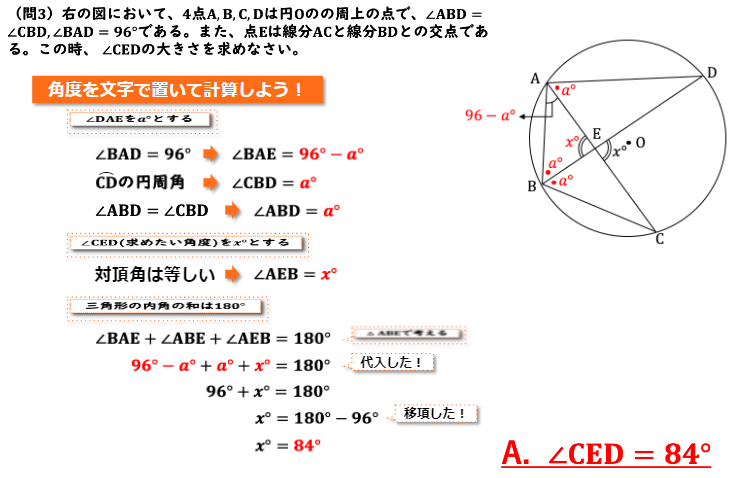
(問3)図において、4点A,B,C,Dは円Oの周上の点で、∠ABD=∠CBD、∠BAD=96°である。また、点Eは線分ACと線分BDとの交点である。この時、∠CEDの大きさを求めなさい。
弧と中心角と円周角:弧の比から長さと角度を求める 問3 回答と解説
クリックで回答と解説を見る
問3の回答
(問3) 回答
84°
問3の解説
今回求めたい角度∠CEDをx度と置いておきましょう。∠CEDをx度と置くと、∠CEDの対頂角∠AEBもx度であることがわかります。
次に∠DAEをa度と置きます。∠DAEをa度とすると、問題文より∠BADが96度となっているので、∠BAEは96-aということになります。
ここで∠ABEの大きさがわかれば、三角形ABEの内角の和180度ということを使ってxの値が求まりそうですね。なので∠ABEを求められないかな、と考えながら見ていくと、∠DAEは弧CDに対する円周角であることがわかります。なので同じく弧CDに対する円周角である∠CBDもa度となることがわかります。
∠CBDの大きさがわかったので、問題文を見ると∠ABDと∠CBDの大きさが等しい、ということが書かれています。なので∠ABDもa度となることがわかります。
以上より、三角形ABEの内角をすべて文字で表すことができました。なので内角の和は180度という性質を使って96°-a°+a°+x°=180°という式をつくることができます。
これを計算すると96+xは180、そしてx=84となり、∠CEDは84度ということになります。
本日の授業はいかがでしたでしょうか。





















関連記事