問1の回答
(問1) 回答
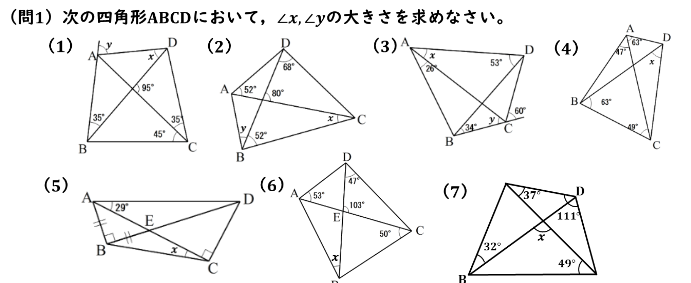
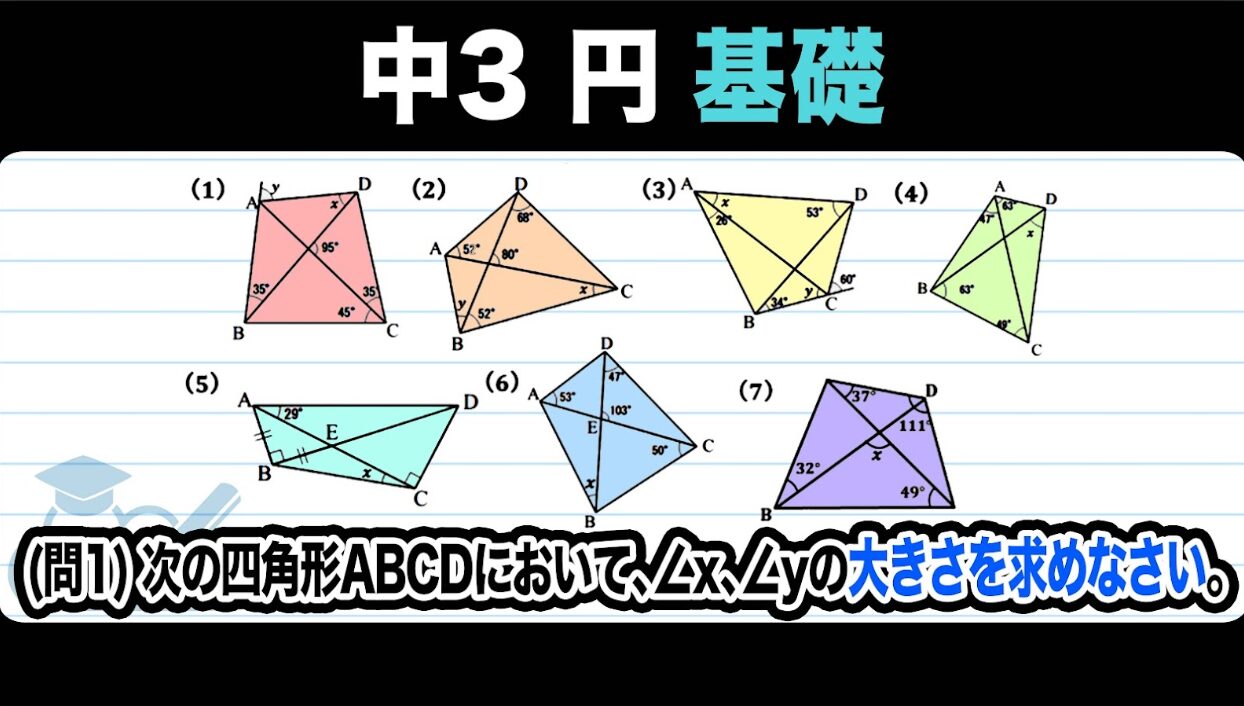
(1) x=45°, y=80°
(2) x=45°, y=80°
(3) x=34°, y=53°
(4) x=47°
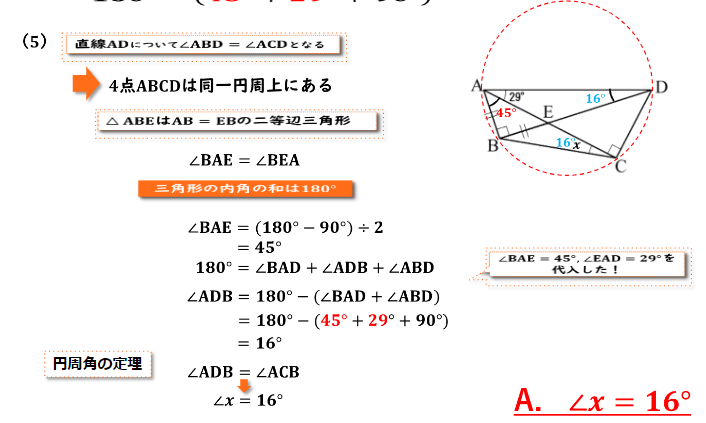
(5) x=16°
(6) x=30°
(7) x=94°
問1 (1)の解説
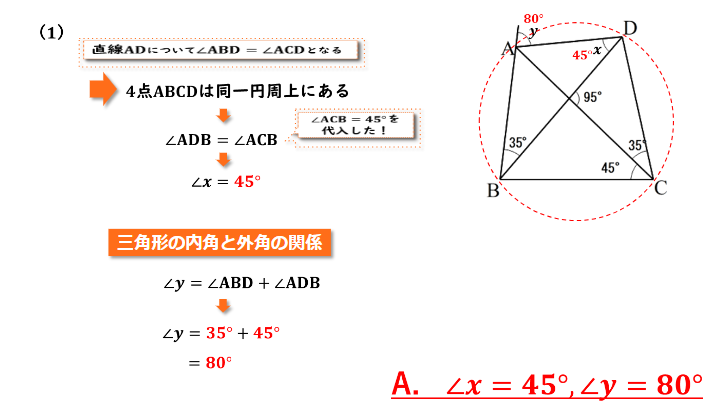
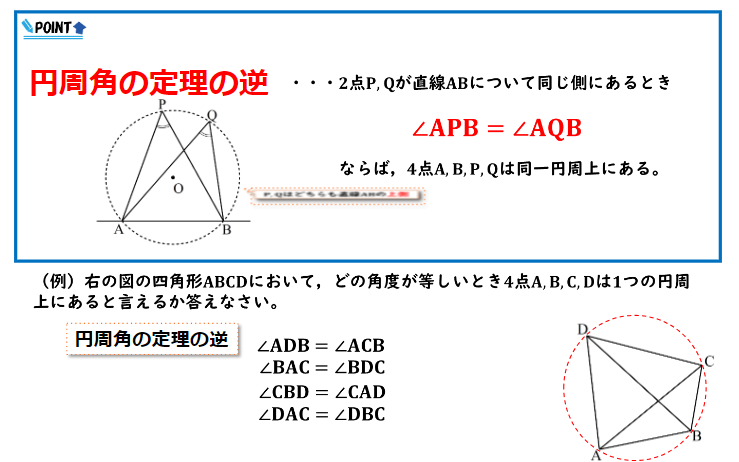
この四角形ABCDを見ていくとまず、直線ADについて∠ABDと∠ACDは同じ35度であることがわかります。
円周角の定理の逆が問題文で用いられている時は問題文で問われている図形の中に、同じ角度の角が2つ存在しているケースが多いのでそこに注意して見るようにしましょう。
そして直線ADについて点Bと点Cはどちらも直線ADの下側に位置しており、∠ABD=∠ACDであることから4点A,B,C,Dは同一円周上にあるということがわかります。
4点A,B,C,Dが同一円周上にあることか弧ABに対する円周角の大きさは等しくなることがわかるので、∠ADB=∠ ACDであることが言えます。これは円周角の定理でしたよね。このように今回の問題は円周角の定理の逆が使えたことから、円周角の定理を用いるといった流れになっていることが分かりますね。
そして∠ACBは45度であると図に記載されているので、∠ADBの大きさ、つまり∠xの大きさは∠ACBと同じ45度になるということが分かります。
∠xの大きさを求めることができたので、次に∠yの大きさを求めていきましょう。
今回は三角形の内角と外角の関係を用います。∠yは三角形ABDの外角であるので、外角の性質から∠yが接していない角度である∠ABDと∠ADBの大きさの和が∠yであるということが言えます。
そして∠ABDの大きさは図に35度と記載されており、∠ADBの大きさは先ほど45度であると求めたので、∠yの大きさは35度+45度=80度。
よって答えは∠x=45度、∠y=80度となります。
問1 (2)の解説
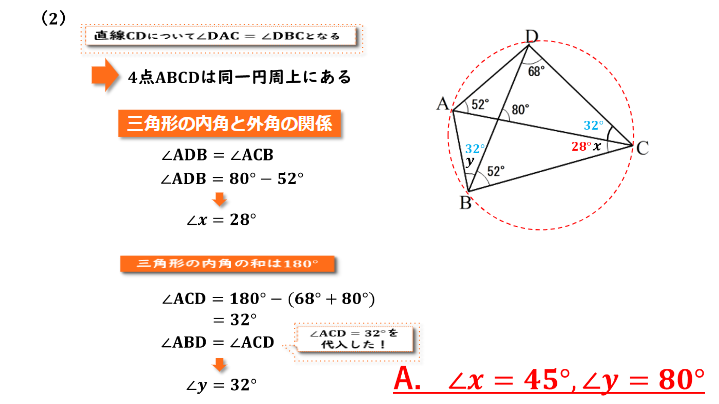
今回は∠DACと∠DBCがどちらも52度となり等しくなっていることがわかります。
直線CDについて点Aと点Bはどちらも直線DCの左側に位置しており、∠DAC=∠DBCなので、円周角の定理の逆から4点A,B,C,Dは同一円周上にあると言えます。
4点A,B,C,Dが同一円周上にあることから弧ABから伸びる円周角である∠ADBと∠ACDも等しいということが言えます。
また三角形の内角と外角の関係から∠ADBの大きさは外角である80度から2つの内角のうちの1つである∠DACを引いた大きさになります。式は右の通りです。∠ADB=80-∠DAC。∠DACは52度なので、∠ADBの大きさは28度となり、先ほど4点A,B,C,Dが同一円周上にあることから∠ADBの大きさと∠ACD(∠x)の大きさが等しいということが言えていたので∠xの大きさも28度となります。
∠xの大きさを求めることができたので、次に∠yの大きさを求めていきましょう。
ここで三角形ACDに着目していくと、すべての三角形の内角の和は180度であるという性質から∠ACDの大きさは、三角形の内角の和180度から、∠BDCの大きさである内角68度と、真ん中の点をPと置くと∠CPDの大きさである内角80度を引いた値となります。式は∠ACD=180-(68+80)。よって∠ACDの大きさは32度であると分かりました。
そして弧ADに着目していくと、弧ADから伸びた2つの円周角である∠ABD(∠y)と∠ACDの大きさは等しいということが分かります。よって∠y=32度であるとわかりました。
よって答えは∠x=28度、∠y=32度となります。
問1 (3)の解説
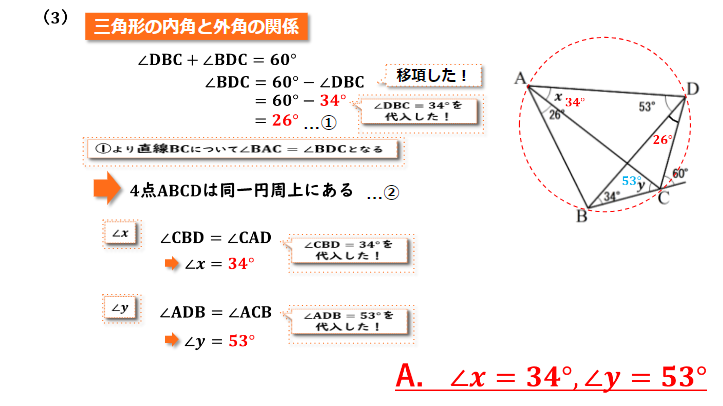
三角形BCDに着目していくと、三角形の内角と外角の関係から、この三角形の2つの内角である∠BDCと∠DBCの和は∠BCDの外角である60度と等しくなります。∠DBCは34度なので、∠BDC+34=60となり、∠BDC=26度であるということがわかりました。
そして直線BCの上側に∠BACと∠BDCというどちらも26度である2つの角を見つけることができたので円周角の定理の逆から4点A,B,C,Dは同一円周上にあるということが言えます。
そして4点A,B,C,Dは同一円周上にあることが言えたので、∠xの大きさを求めることができます。
今回は CDに着目していくと、弧CDから伸びた2つの円周角である∠CAD(∠x)と∠CBD が等しいということが言えます。よって∠xの大きさは34度となりました。
最後に∠yの大きさを求めていきましょう。∠yも∠xと同様の考え方で大きさを求めることができます。
今回は弧ABに着目していくと弧ABから伸びた2つの円周角である∠ADBと∠ACB(∠y)の大きさが等しいことがいえます。∠ADBは53度なので、∠yの大きさも53度となります。
よって答えは∠x=34度、∠y=53度となります。
問1 (4)の解説
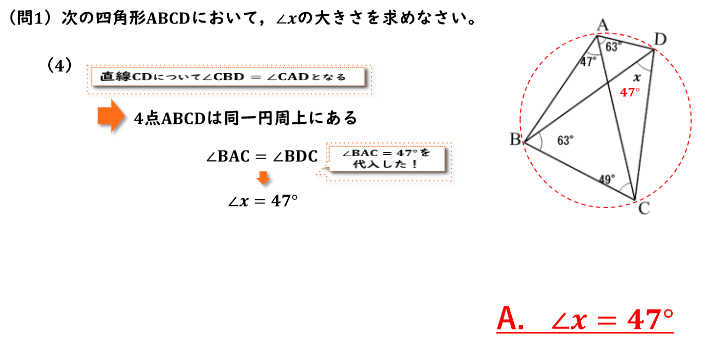
図から∠CBDと∠CADの大きさがどちらも63度となっていることがわかると思います。
そしてこの2つの角度が直線CDについて点A,Bが直線CDの左側にどちらも位置しているので、円周角の定理の逆から4点A,B,C,Dは同一円周上にあるということが言えました。
よって弧BCに着目していくと弧BCから伸びた2つの演習角である∠BACと∠BDC(∠x)の大きさは等しいということが言えます。∠BACは47度なので∠xも47度であるとわかります。
よって答えは∠x=47度となります。
問1 (5)の解説
この図形を見て、大きさが等しい2つの角度なんてどこにもないじゃないか、と思った方は要注意!
今回は∠ABDと∠ACDがどちらも直角である、つまり90度となっているため、この2つの角の大きさが等しいと いうことが言えます。そして直線ADについて点B,Cはどちらも直線ADの下側に位置しているので4点A,B,C,Dは同一円周上にあることがわかります。
今回は∠xを求めるために∠ADBの大きさを求める必要があります。そのため三角形ABDの周辺の角度を求めていきましょう。今回の三角形ABEを見ていくとAB=EBであることがわかるため、三角形ABEは二等辺三角形であるということがわかります。二等辺三角形の2つの角は等しいので∠BAE=∠BEAそしてすべての三角形の内角の和は180度であるため∠BAE=∠BEA=45度であるとわかります。∠BADは∠BAE+∠EADの和であるため、∠BAD=45+29となり、∠BADは74度とわかります。
よって三角形ABDに着目していくと、三角形の内角の和は180度となるため、∠BAD+∠ADB+∠ABD=180となります。∠BAD=74、∠ABD=90なので
74+∠ADB+90=180これを解くと、∠ADB=16度であると分かります。
そして円周角の定理から弧ABに着目していくと、この ABから伸びた2つ 円周角である∠ADBと∠ACB(∠x)は大きさ が等しくなるので、∠xの大きさも16度となります。
よって答えは∠x=16度となります。
問1 (6)の解説
ここまで問題を解いてきた皆さんなら∠ABD(∠x)と∠ACDが等しければ∠xが求められるだろう、という発想を持つことができるのではないでしょうか。実際円周角の定理の逆を用いて問題を解いていく際には、どの2つの角が円周角となるか、という視点を持つことが重要です。
まずは四角形ABCDの、点A,B,C,Dの4点が同一円周上にあることを示すために2つの等しい角を見つけていきたいところですね。ここでは∠ADBと∠ACBが等しいのではないかといった予想ができると思います。
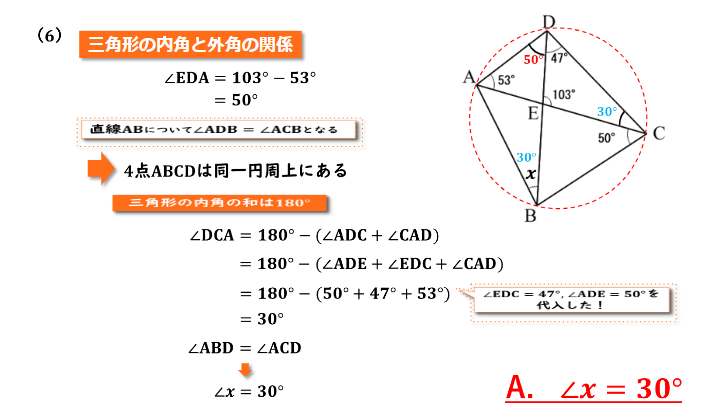
そこで今回は三角形ADEに着目していくと、∠ADE(∠ADB)の大きさは外角である103度からもう一方の内角∠DAEの53度を引いた大きさとなるの∠EDA=103-53となり、∠ADE(∠ADB)の大きさは50度となります。
よって∠ADBは50度であり、図より∠ACBも50度であることも分かっています。直線ABについて点C,Dはどちらも直線ABの右側に位置しているので、4点A,B,C,Dは同一円周上にあるということが言えました。
このことから∠ABD(∠x)と∠ACDは同じ弧ADから伸びた円周角となっているので、∠ACD(∠ECD)の大きさを求めることができれば、∠xの大きさを求かけられるということになります。
ここで三角形ACDに着目していくと、すべての三角形の内角の和は180度であることから、
∠DCA=180-(∠ADC+∠CAD)と式を立てることが出来ます。∠ADC=∠ADB+∠BDC=50+47=97、∠CAD=53なので、
∠DCA=180-(97+53)よって、∠DCA=30度となります。
そして円周角の定理から弧ADに対する円周角の大きさが等しいので、∠ABD(∠x)と∠ACDの大きさは等しいので、∠xの大きさも30度となります。
よって答えは∠x=30度となります。
問1 (7)の解説
今回は∠ABDと∠ACDの大きさが等しいことが言えれば、4点A,B,C,Dが同一円周上にあることが言えますね。そして∠ACDの大きさは三角形の内角の和が180度であること∠ACD=180-(∠DAC+∠ADC)となり、これを解くと∠ACD=32度となることが分かります。
これで、先ほど立てた予想通り∠ABDと∠ACDの大きさが等しくなりましたね。 また、直線ADについて点B,Cはどちらも直線ADの下側に位置しているので、4点A,B,C,Dは同一円周上にあるということが言えました。
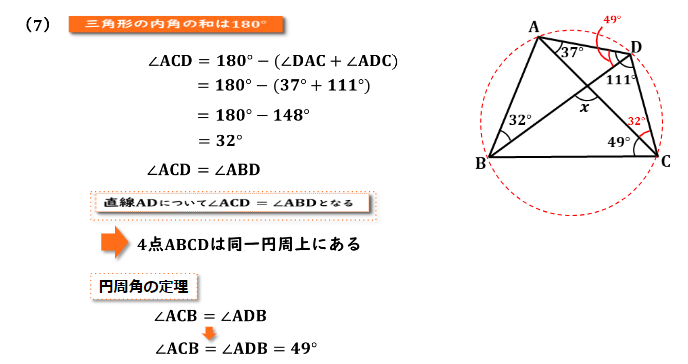
4点A,B,C,Dが同一円周上にあることからABから伸びる円周角∠ACBと∠ADBは等しくなることが分かります。よって∠ADBの大きさは49度になります。
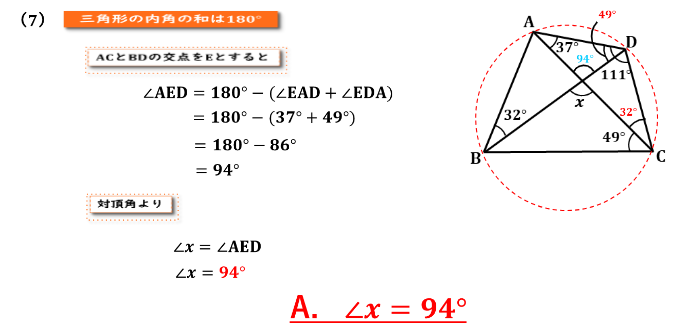
また ACとBDの交点をEとすると、三角形AEDの内角の和が180度であることから、
∠AED=180-(∠EAD+∠EDA)となります。∠EAD=37、∠EDA=49なので、式に代入すると∠AEDは94度となります。
∠xは∠AEDの対頂角であることから∠x=∠AEDという式が成り立つので∠xの大きさも94度となります。
よって答えは∠x=94度となります。























関連記事