今回は密度について解説していきます。
密度の学習は中学理科の中でも確実に抑えておかなければならない分野です。
しかし、実際は密度の正しいイメージを持てておらず困っている人も多いと思います。
そこで今回は、人口密度や卵の浮き沈みと言ったイメージのつきやすい例を交えながら密度についての理解を深めていきたいと思います。
語句の確認
密度を学ぶ前にまずは今回使う語句の整理をしていきましょう！
この場合の単位は「グラム毎立方センチメートル（ g / ㎤ ）」になります。
質量…場所によって変化しない物体そのものの量。単位は「グラム（g）、キログラム（㎏）」
※ここで注意すべきは質量と重さの違いです。重さは物体に働く重力のことなので、質量と重さを混合しないようにしましょう。
密度とは
皆さんも同じ大きさの物なのに持った時に感じる質量が違うことに疑問を持ったことがあると思います。
例えば、同じ大きさの「石」と「発泡スチロール」。もっと言えばこの2つと同じ大きさの「風船」。なぜ大きさは同じなのに質量が違うのでしょうか？
答えは簡単で密度が異なるからです！
物体の質量の計算は密度(g/㎤)×体積(㎤)=質量(g)です。
同じ大きさ…つまり同じ体積であればこの計算式からも密度が大きくなれば質量も大きくなりますね！
はじめに出した人口密度の例で考えてみましょう。
「1人が暮らしている家」と「100人が暮らしている家」家が全く同じものだったらどちらが重そうですか？
100人の方ですよね！これが密度による質量の変化です！
もっと簡単に言うと見た目は同じ大きさの家なのに（見た目は同じ大きさの石と発泡スチロール）質量が違うのは中身の詰まり具合が異なるから！1人より100人の方が家の中身が詰まってますよね。
（図1）
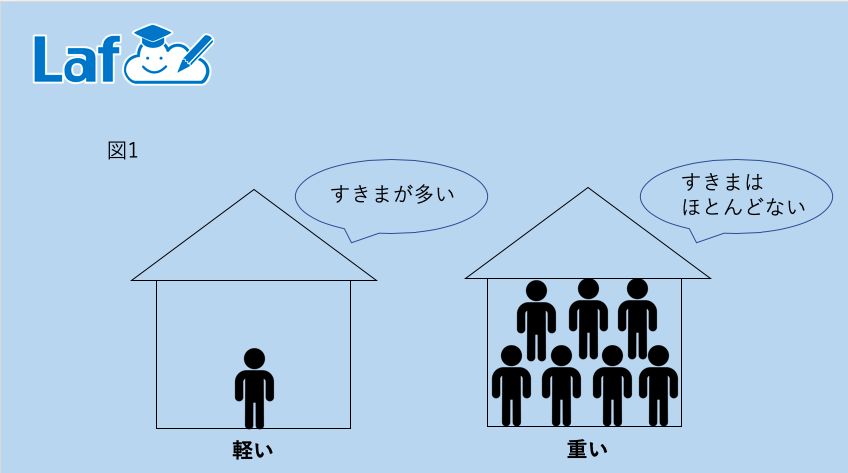
この図と同じことが石と発泡スチロールで言えます。石を割ってみると中身は、、だいぶ詰まっていますよね！（隙間ほとんどなし）逆に発泡スチロールは空気がものすごくたくさん入っています（隙間いっぱい）。風船に限ってはもう空気しか中見ないですよね。これらの密度の違いで物体の大きさが同じでも質量が違ってくるのです！
浮き沈み
次に密度を使って身の周りのことを考えてみましょう！
石は水に浮きますか？浮きませんよね。
では、なぜ浮かないのかを考えたことありますか？
石が水に浮かない理由も密度の差で説明ができます。
水にも密度があり、その密度よりも石の密度が大きいから水の中に石が沈むのです！
では、発泡スチロールはどうでしょう？発泡スチロールは浮きますよね！想像してみてください。
発泡スチロールが水に浮く理由は発泡スチロールの密度が水の密度よりも小さいからですね！
この性質を用いた面白い実験があるので以下をみてみましょう。
新鮮な生卵を水の中に入れると、、沈みます。
ではこの生卵を浮かせたいなぁって思った時あなたならどうしますか？先に答えを言ってしまうと水に塩を入れて塩水にしてしまうのです！
ではなぜ塩を入れるのでしょうか…？
水に塩を入れると溶けますよね！塩を水に溶かすことによって液体の密度を大きくすることが出来ます！そうすると卵の密度を塩水の密度が追い越し、沈んでいた生卵が浮き出してくるのです！
（図2）
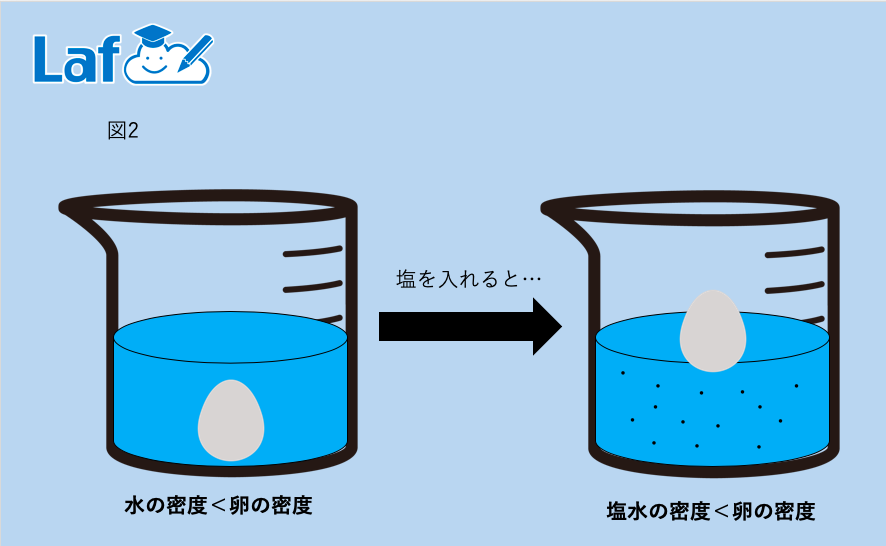
野菜などでも試せると思うので是非自分で実験してみてください。
密度の計算の仕方
さてイメージがついてきたところで本題の密度の計算の仕方を学んでいきましょう！
先ほども出しましたが密度の計算は
密度(g/㎤)=質量(g)÷体積(㎤)で表せます。
密度はある空間において平均（正確には単位量当たり）でどのくらいの量があるのかを定量的に表した値です。つまり体積の単位をリットル(L)や立方キロメートル(㎦)に置き換えても計算ができます。
この計算式は体積だけでなく面積などにも応用できます。例えば、都道府県の人口密度は単位面積当たり（1㎡）の人口を出しているわけです。
人口密度(人/㎡)=県民数(人)÷その県の面積(㎡)
単位の種類としては無数にあります。
㎏/㎦や㎎/㎟などですね。
要するに何を基準にして何の量を考えたいのかを考えて割り算してあげればいいのです！
ちなみに（g/㎤）の密度の単位の読み方「グラム毎（まい）立方センチメートル」ですが、毎は「ごと」とも読めますよね。つまり1立方センチメートルごとに何グラムあるのか…ということですね！（注．逆と誤解しないように気を付けてください）そうやって理論的に覚えてしまえば、割る方を間違えてしまう…なんてミス起きないですよね！では、また次回お会いしましょう。
