Laf創業・経営8年目【経歴/実績】
・これまで200名以上のお子様の指導実績あり
国公立をはじめとした難関高への進学をサポート
・AI先生をはじめとした日本初の教育サービスを展開
月間3,000人以上が利用するサービスへと育て上げる
AI先生を利用したことで模試C判定からA判定まで上がったと喜びの声も多数
利用者数3,000人突破！
動画解説AI先生
【多角形】多角形の外角の和の求め方 解説動画
本日は中2数学 平行線・多角形・合同 多角形の外角の和の求め方についてやっていきたいと思います！
初めてみる人は外角ってよくわからないって思いますよね。
しかも、参考書の解説がわかりづらくて勉強が嫌になるときありますよね。
今回の動画では参考書ではありえないくらい丁寧に解説していきますので、高評価＆チャンネル登録よろしくお願いします！
それでは本日の問題を見ていきましょう！
多角形の外角の和の問題
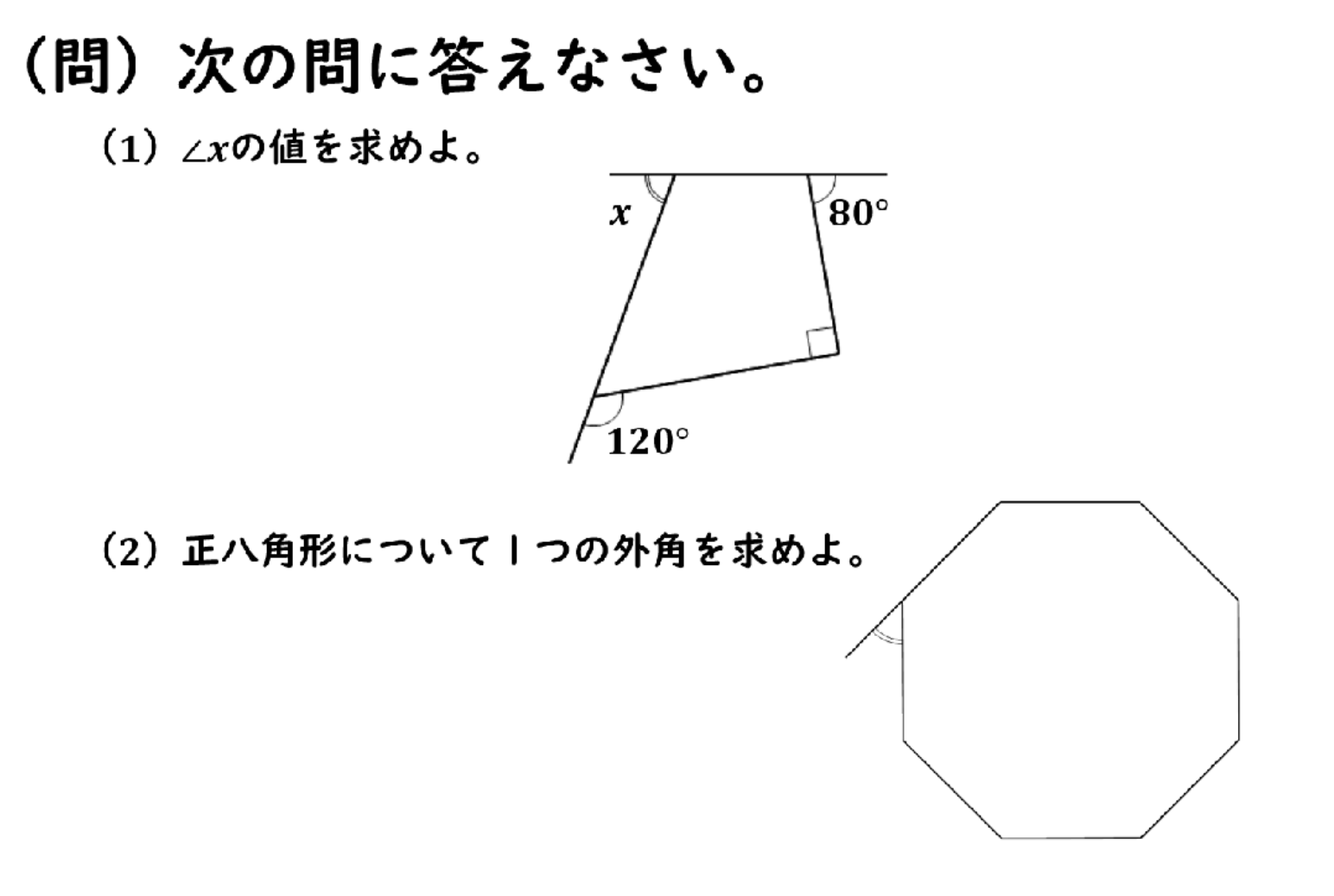
では解いていきましょう！
多角形の外角の和の解説
本日のポイント
外角=180°-(内角)で求めることができます。
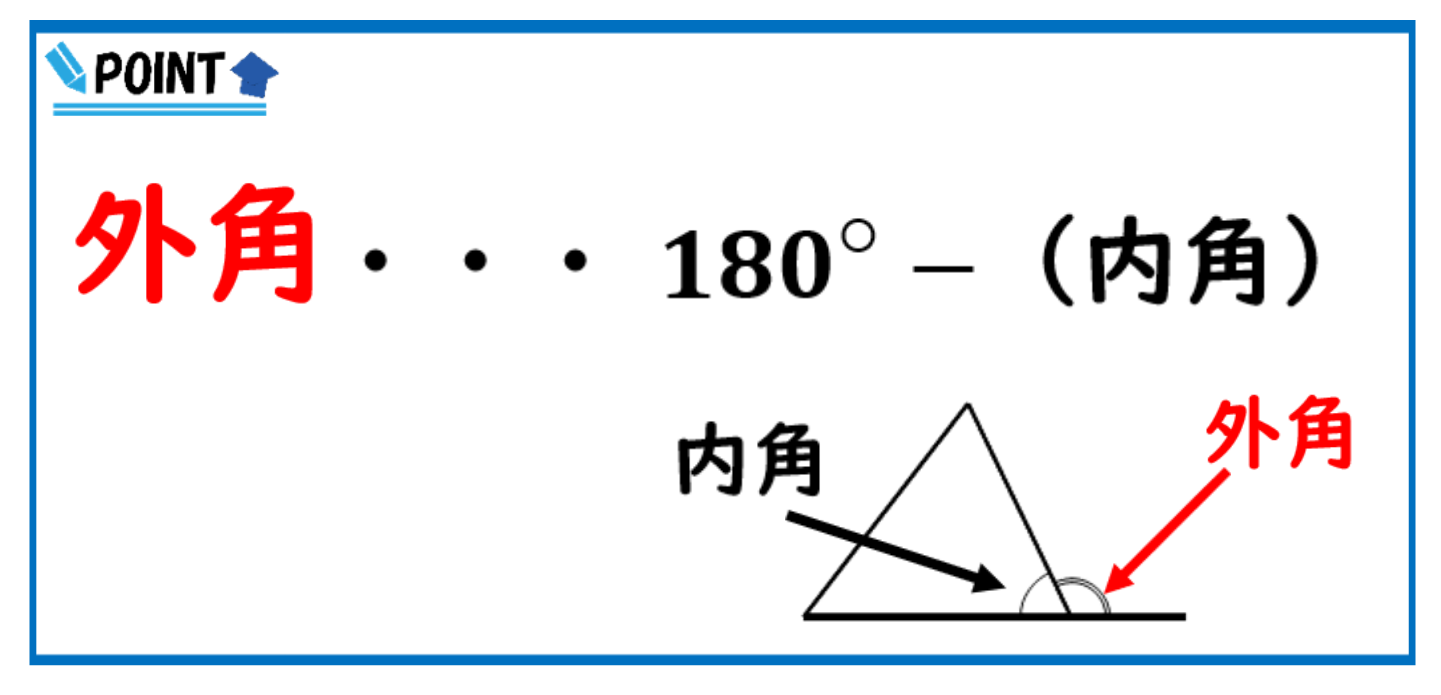
どういうことかというとこの図のように三角形の一辺を伸ばしたとき三角形の内側の角度を内角そしてこの外側の部分を外角と言います。
なので外角は180°から内角を引けば求めることができます。
それでは右図の90°の外角を求めてきましょう！
補助線を付け足してあげるとこのようになりますそれでは外角を計算していくと外角は180°から内角を引けば求めることができるので180°-90°となりまず計算をしてあげると90°の外角は90°であるということがわかりました。
なので図にも90°と書いてあげましょう！
それではここまできたらもう一つのポイント外角の性質について説明していきたいと思います。
外角の性質はこちらになります。
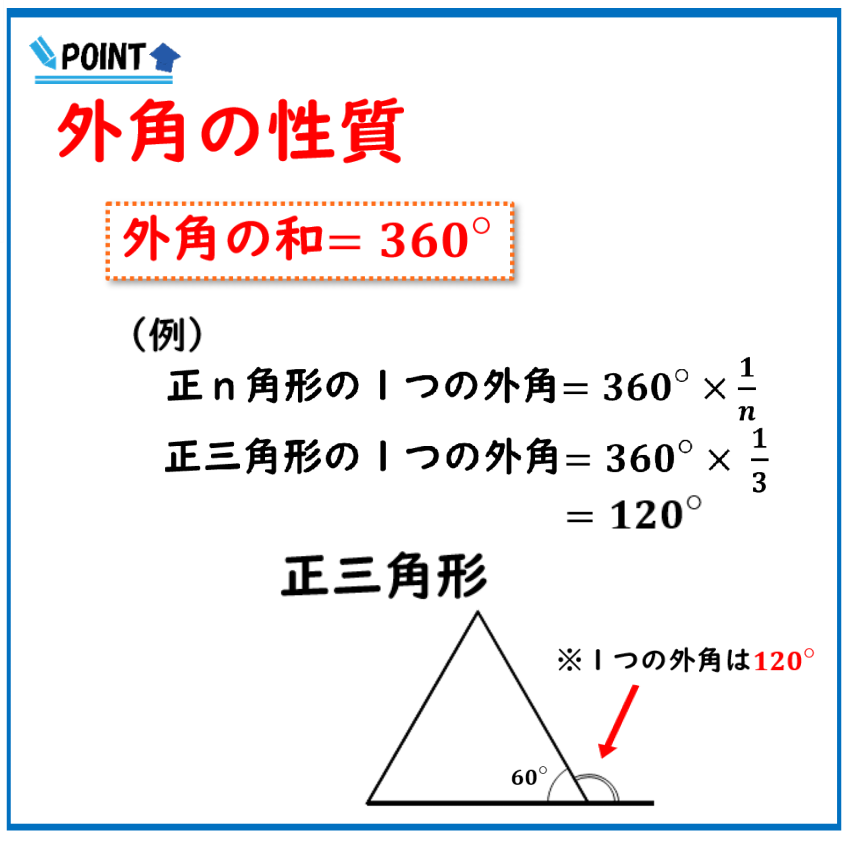
どんな多角形でも外角の和は360°になります。
それでは例を見て説明していきたいと思います。
正ｎ角形の１つの外角は360°×1/ｎで求めることができます。
なぜかと言うと外角の和が360°なので正ｎ角形の場合は頂点がｎ個あります。
なので外角もｎ個あるので１つの外角を求める時は360°をｎで割ってあげる
すなわち1/n倍してあげれば求めることができます。
もう１つ例を見ていきましょう正三角形の１つの外角は360°を３で割ってあげる
すなわち1/3倍してあげればいいので計算をしてあげると120°であるということがわかります。
図に表してあげるとこのようになります。
正三角形の内角は60°であり外角はこちらになります。
こちらが120°であるということがわかりました。
多角形の外角の和の解説(1)
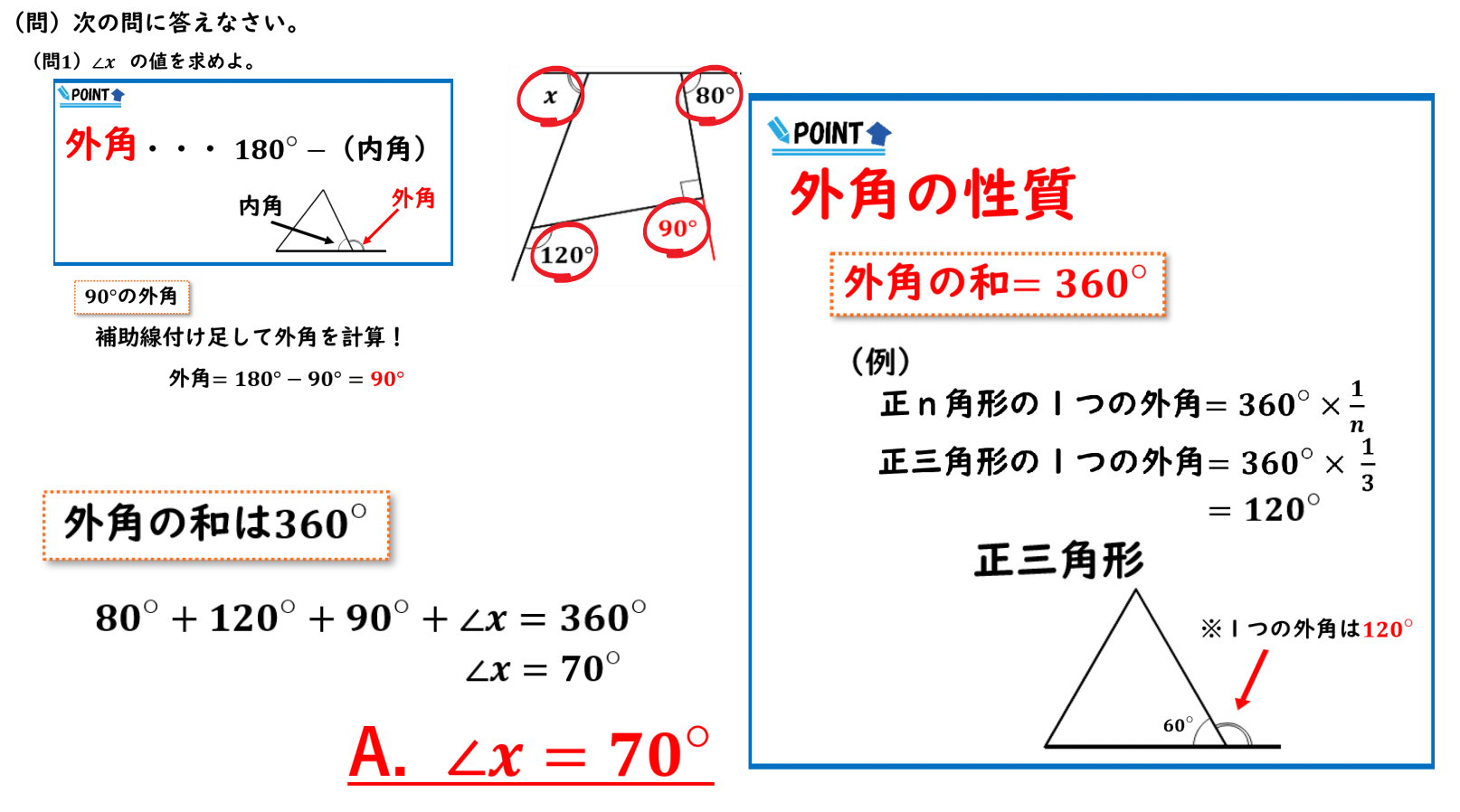
外角の性質から外角の和は360°であるということはわかっているので今回の図形の外角をチェックすると右上が80°左下が120°右下が90°そして左上がX°であるということが分かるので80°+120°+90°+∠X＝360°になるということがわかります。
こうして計算をしてあげると∠Xは70°であるということがわかりました。
なので答えは70°となります。
多角形の外角の和の解説(2)
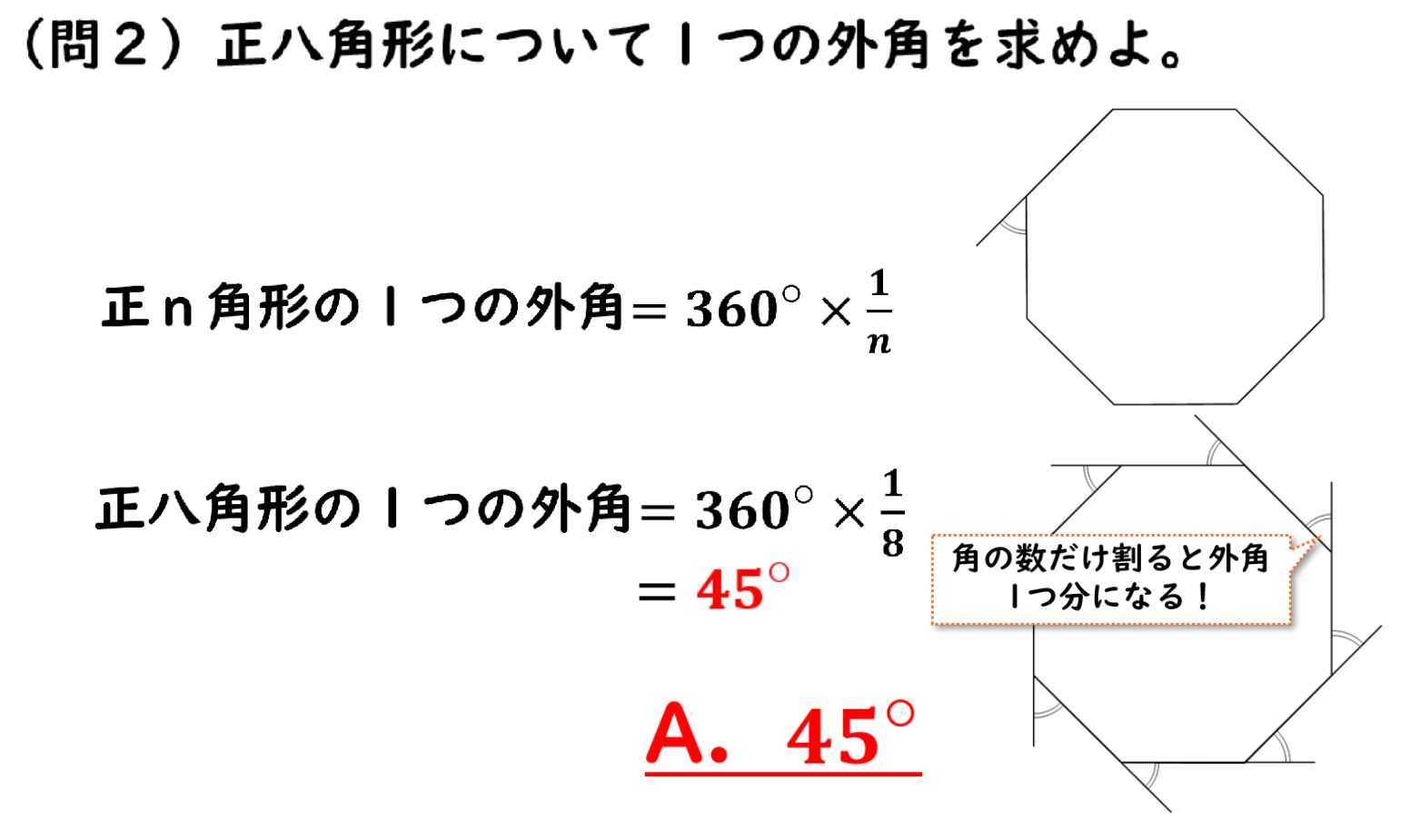
今回正八角形の外角を書いてあげるとこのようになります。
外角の和は360°であり角の数だけ割ると外角１つ分になる！というのは先ほど説明しました。
よって先ほど説明したとおり外角の性質は正ｎ角形の一つの外角は360°×1/nで求めることができるので今回は正八角形と頂点が8つなので360°×1/8となります。
８分割してあげれば求めることができるので計算をしてあげると正八角形の一つの外角は45°であるということがわかりました。
なので答えは45°となります。
本日のポイント
外角とは一辺を延長した時にできる角になります。
(外角)=180°-(内角)
外角の性質は外角の和=360°
これだけ覚えておきましょう！
多角形の外角の和の練習問題
本日の授業はいかがでしたでしょうか？
出来た！ 出来ない…！などコメントで教えてください！
数学の勉強について悩んでいる人向けに公式LINEで質問に答えているのでこちらから友達追加お願いいたします！
これからも参考書のざっくりとした解説で困らないように丁寧に解説していきますので高評価とチャンネル登録よろしくお願いいたします！
本日もご視聴ありがとうございました！
コメント一覧