【円】弧と中心角と円周角！弧の比から円周角を求めて角度を求める！をわかりやすく解説！【中3数学】1 min read

 問の回答

問の解説

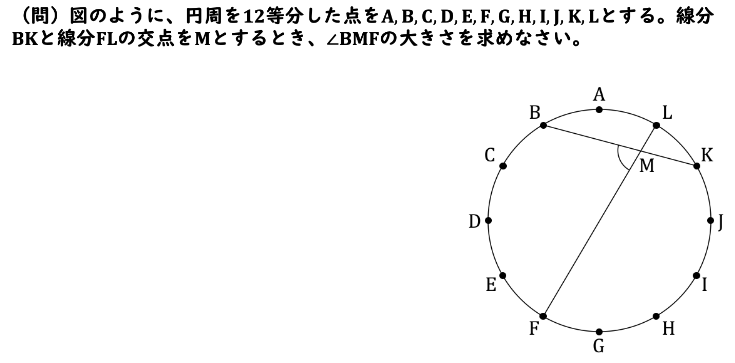
線分BKと線分FLの交点をMとするとき、∠BMFの大きさを求めなさい。の解説をしていきます。

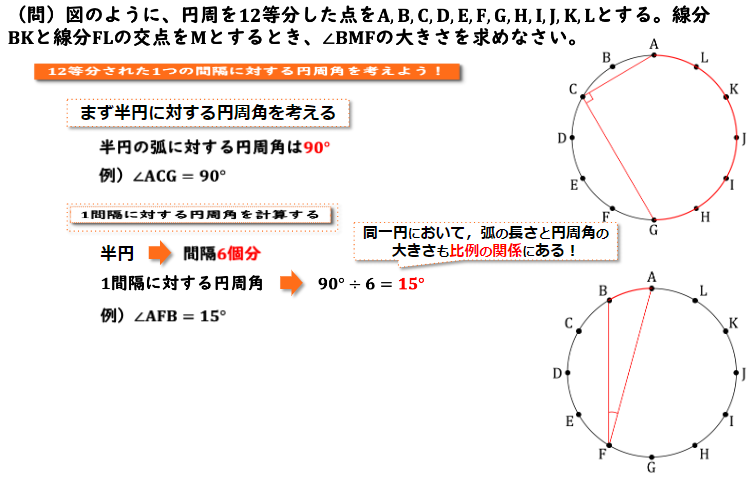
12等分された1つの弧（例えば弧ABや弧BCなど）に対する円周角について考えていきましょう。

まずは半円に対する円周角を考えましょう。例えば半円の部分である弧AGから出ている円周角∠ACBについて考えてみます。すると∠ACBは90度だとわかります。なぜかというと、点A から点Gに直線を引っ張った時に、直線AGはこの円の直径になります。直径から出る円周角は90度となりますよね。こちらはしっかり覚えておきましょう。

つまり12等分された弧が6個分のとき、円周角は90度になることが分かりますよね。

それでは、この12 等分された1つの弧に対する円周角を計算してきましょう。
12等分された弧が6個で円周角は90度、では12 等分された弧が1個で円周角は何度になるか、ということです。

円周角の定理より、弧の長さと円周角は比例の関係にあるので、もとめたい12 等分された弧が1個で円周角をxとすると、
6:90=1:xという式が立てられます。これを解くと
↓
6x=90
↓
x=15
つまり12 等分された弧が1個で15°ということになります。たとえば弧ABの円周角は15°になるということです。

それでは三角形BMF使って今回求めたい角度を求めていきます。

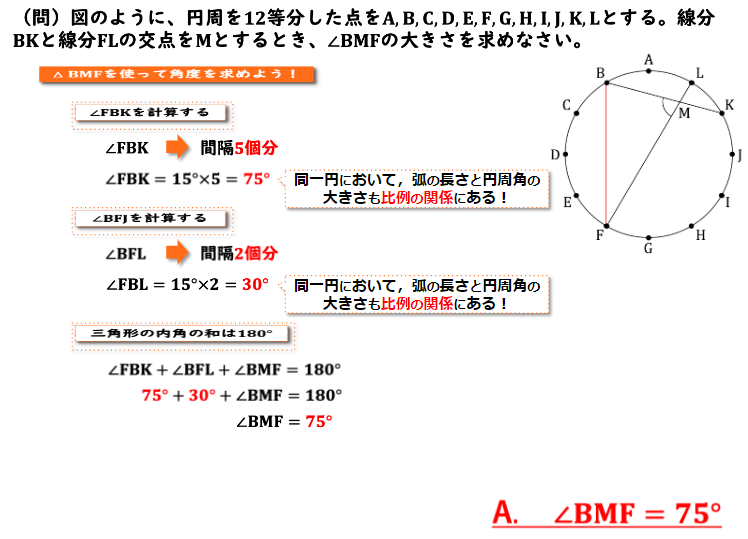
まずは∠FBKから求めていきましょう。∠FBKを円周角とする弧FKの長さは数えてみると、12等分された弧が5個分ということがわかります。よって先ほど求めた通り1個あたりの円周角が15度なので、
∠FBK=15°×5個分となり、∠FBK=75°であるということがわかります。

それでは同様に∠BFJも求めていきます。∠BFJを円周角とする弧BJの長さは数えてみると、12等分された弧が2個分ということがわかります。よっ て
∠BFJ=15°×2個分となり、∠FBK=30°であるということがわかります。

これで三角形BMFの2つの内角が分かったので、三角形の内角の和が180度になることを活用して∠BMFを求めてきます。

式は∠BMF=180°-(∠FBK+∠BFJ)となり、∠FBK=75°、∠FBK=30°なので
∠BMF=180°-(75°+30°)
↓
∠BMF=180°-105°
↓
∠BMF=75°

よって∠BMFの大きさは75°となります。