因数分解について教えて！
中学三年生になって最初の難関。因数分解。
覚えることが多く、以前習った内容も使うためここで授業についていけなくなったという方も多いのではないでしょうか？
今回はそんな因数分解を完璧にするため、因数分解を徹底的に解説してきます！
因数分解にまだ不安が残る方や全く分からないという方は是非チェックしてください！
Laf創業・経営8年目【経歴/実績】
・これまで200名以上のお子様の指導実績あり
国公立をはじめとした難関高への進学をサポート
・AI先生をはじめとした日本初の教育サービスを展開
月間5,000人以上が利用するサービスへと育て上げる
AI先生を利用したことで模試C判定からA判定まで上がったと喜びの声も多数
「話題沸騰中！16大メディアが注目したLaf先生AI – あなたの学びをもっと身近に」
各社が報じた話題のAI教育ツール。24時間質問し放題、理解度に応じた解説で、わからないをゼロに。今すぐ試して、学びを加速させよう。
※様々なメディア様に注目いただき、反響多数！現在TV取材も予定している注目サービスとなっています。（一部掲載）
因数分解とは
そもそも、因数分解とはなにか。
どのようなことをするのかから解説していきます。
数学が苦手だ・まだ習っていないという方は、「因数分解とは」の解説から見始めてください！
因数分解より前に習う範囲の復習もしながら簡単に説明していきます！
因数分解とは
因数分解とは、文字通り因数に分解することです。
では、因数とは何でしょう？
因数とは、「積を構成する数字」のことです(積は掛け算の答え)
例えば、12という数字があったとき、掛け算で12を作ろうと思うと1×12, 3×4, 2×6の3パターンがあります。
1×12の場合は1と12が、3×4の場合は3と4が因数になります。
そして、このように「積を因数に分解すること」が因数分解という行為です。
数学では積と因数が単純な整数ではなく、単項式や多項式になったものをいわゆる因数分解と呼んでいます。
教科書には「因数分解とは多項式を2つ以上の単項式や多項式の積の形で表すこと」というふうに書いてありますが、簡単に言うと、「掛け算と足し算の式（積）を掛け算だけの式（因数）に直すこと」です。
【復習】単項式、多項式とは
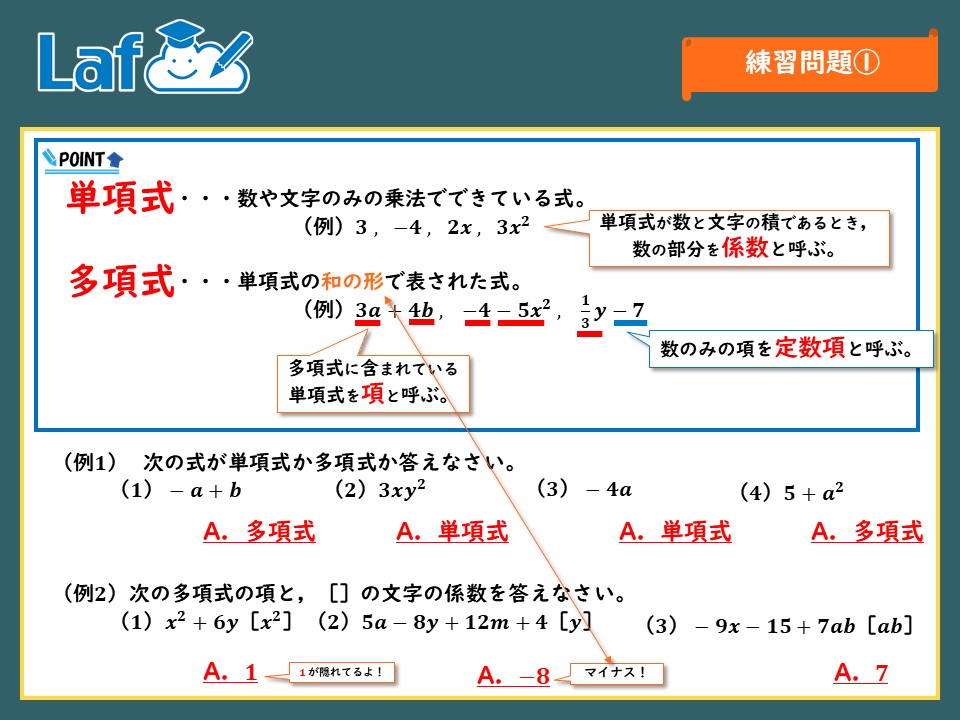
単項式と多項式の復習です。理解している方は飛ばして構いません。
単項式とは文字と数字を使った掛け算のみの式のことです。
そもそも「項」とは「+で挟める数字」のことです。
5-4+3という式があったとき、項は5と-4と3になります。
分かり易い式に直すと5+(-4)+3になりますね。
この「項」が一つだけの式を単項式といます。
では、2aという単項式にはどんな計算が隠されているでしょうか。
2×a=2aですね。このように単項式は掛け算のみの式になっていることが分かります。
一方、多項式とは文字と数字を使った掛け算と足し算のある式のことです。
文字の通り、項が複数ある式になります。
先ほどの例で言うと、2a他に3bという項が含まれるとします。式は2a+3bになりますね。
つまり足し算の要素が式に加わります。
復習は以上です！これから、この多項式を使った乗法公式と因数分解のやり方を解説していきます！
「わかりやすい授業動画」と「練習問題で理解を深めたい方」はコチラ！
＞中2の復習！単項式と多項式【中3数学：式の展開と因数分解】
因数分解の流れとパターン
因数分解には公式があります。
公式を使えれば因数分解は楽勝です。
それぞれの公式とその特徴をしっかり覚えていきましょう！
共通因数をくくる
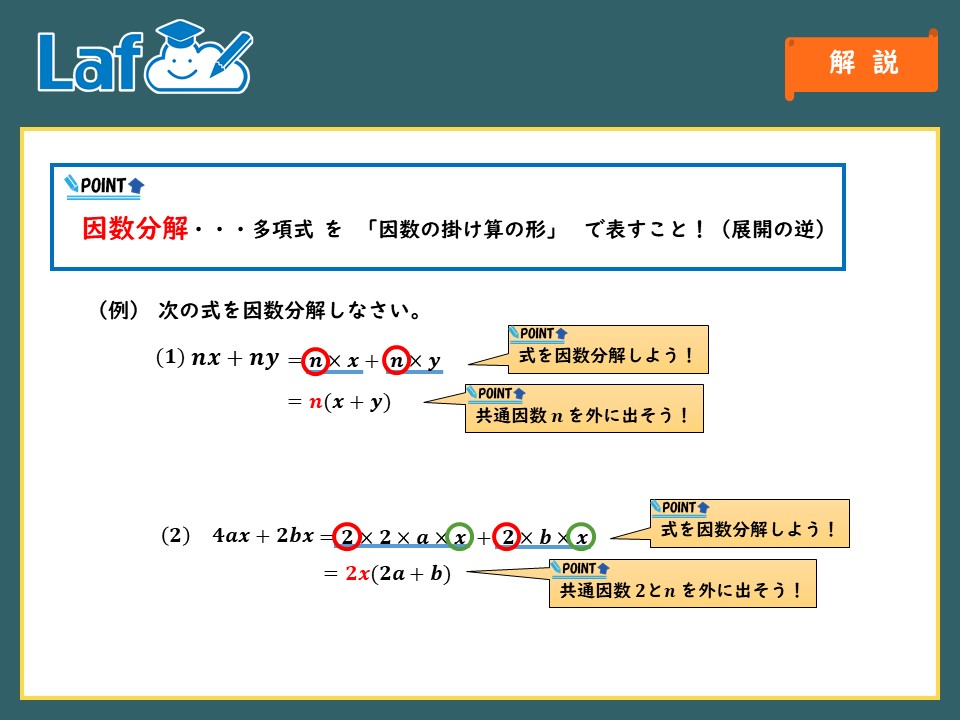
因数分解には公式があると言いましたが、公式は決まったパターンにしか適用できません。
与えられた式を、公式が適用できる形に変えるために共通因数でくくるという作業をする必要があります。
共通因数でくくるとは「共通している因数を外に出してまとめる」ということです。
例えば、2ac+2bcという式を共通因数でくくるとします。
2acの因数は2, a, c で、2bcの因数は2, b, c です。
この二つは2とc という因数を共通して持っています。
よって、2c(a + b)と表すことが出来ます。
2c(a + b)=2ac + 2bcになりますね。
「わかりやすい授業動画」と「練習問題で理解を深めたい方」はコチラ！
＞因数分解：共通因数をとり出す！【中3数学：因数分解】
因数分解の公式
因数分解の公式は以下の四つのみです！
それぞれの式の形と、違いを覚えておきましょう！
x² + (a + b)x + ab = (x + a) (x + b)
x² + 2ax + a² = (x + a)²
x² – 2ax + a² = (x – a)²
x² – a² = (x + a) (x – a)
以下ではこれらの公式を例題を使って説明してきます！
公式① x² + (a + b)x + ab = (x + a) (x + b)
(x + a) (x + b)の形に因数分解することが出来るとき、
xの係数は(a + b)、定数項（文字の掛かっていない数字）はab になります。
展開するとx² + bx + ax + abとなり、bxとaxを共通因数xでくくるとx² + (a + b)x + abとなりますね。
例：x² + 5x + 6 を因数分解する。
a + b =5, ab = 6になるような数字を探します。
先に積が6になる組み合わせをさがします。
積が6になる組み合わせは1×6, 2×3があります。
このうち、和が5になる組み合わせは2 + 3のときですね！
よって、解答はx² + 5x + 6 = (x + 2) (x + 3)となります。
例２：x² + 4x – 21を因数分解する。
公式②には、定数項が負の数になっている場合があります。
しかし、計算方法は変わりません。
a + b = 4, ab = -21になる組み合わせを探します。
積が-21になるのは1×21, 3×7のそれぞれどちらかの因数が負の数の場合です。
このうち、和が4になるのは(-3) + 7の組み合わせの場合です。
よって、解答はx² + 4x – 21 = (x + 7) (x – 3)となります。
例3：x² – 7x – 18を因数分解する
公式①にはｘの係数が負の数になっている場合があります。
やはり、計算方法は変わりません。
a + b = -7, ab = 18になる組み合わせを探します。
積が18になる組み合わせは18×1, 2×9, 3×6があります。
このうち、和が-7になるのは(-9) + 2の組み合わせの場合です。
よって解答はx² – 7x + 18 = (x – 9) (x + 2)となります。
「わかりやすい授業動画」と「練習問題で理解を深めたい方」はコチラ！
＞因数分解：x²＋(a+b)x＋ab = (x+a)(x+b)【和と積の公式！中3数学】
公式② x² + 2ax + a² = (x + a)²
(x + a)²の形に因数分解することができるとき、xの係数は2a、定数項はaの2乗になります。
公式を覚えていなくても(x + a) (x + a)を展開すると、x² + ax + ax + a²となり、x² + 2ax + a²となりますね。
例：x² + 24x + 144を因数分解する
定数項144は12の2乗、xの係数は12の2倍(2a)になっています。
よって、解答は(x +12)²となります。
例2：4x² + 12x + 9を因数分解する
公式③では、xの係数が1でない場合があります。
しかし、考え方は変わりません。
定数項9は3の2乗、4x²を(2x)²と考えるとxの係数は3の2倍に2xを掛けたものとかが得られます。
よって、解答は(2x + 3)²となります。
公式③ x² – 2ax + a² = (x – a)²
(x – a)²の形に因数分解することができるとき、xの係数は-2a, 定数項はaの2乗になります。
公式②の(x + a)²とはxの係数の正負が違います。
例：x² – 26x + 169を因数分解する
定数項169は13の2乗、xの係数は13の2倍(2a)になっています。
よって、解答は(x – 13)²となります。
公式④ x² – a² = (x + a) (x – a)
(x + a) (x – a)の形に因数分解することができるとき、x² – a²の形になります。
式を展開すると、x² – ax + ax + a²となり、xの係数は打ち消し合ってx² – a²だけが残ります。
例：x² – 9を因数分解する
定数項9は3の2乗。
よって解答はx² – 9 = (x – 3) (x + 3)となります。
よく使う数字の2乗
因数分解でよく使われる2乗を覚えておくと便利です！
いちいち筆算する必要がなくなり、テストでも時間の節約になります。1～20まで覚えておけば十分でしょう！
1² = 1
2² = 4
3² = 9
4² = 16
5² = 25
6² = 36
7² = 49
8² = 64
9² = 81
10² = 100
11² = 121
12² = 144
13² = 169
14² = 196
15² = 225
16² = 256
17²= 289
18² = 324
19² = 361
20² = 400
まとめ
いかがでしたでしょうか？
今回は因数分解について、用語の解説から細かく説明していきました！
数学が苦手な人にとって、教科書は不明な単語ばかりで、読む気になれないと思います。
そこで諦めるのではなく、用語を一つ一つ先生に分かるまで聞くというのが大事です！
まずは、自分が納得できる説明を見つけましょう。
より網羅的に勉強したい方向けに
勉強でもっと効率的に成績を伸ばしたいと思いませんか？
そんなあなたにぴったりなのが「スタディサプリ中学講座」です！
なぜスタディサプリなのか？
- トップレベルの講師陣
- 経験豊富な人気講師による分かりやすい授業
- 難関高校合格者を多数輩出した実績ある講師陣
- 豊富な教材と動画コンテンツ
- 5教科をカバーする充実の講義動画
- インタラクティブな練習問題で理解度をチェック
- 自分のペースで学習可能
- いつでもどこでも、スマホやタブレットで学習
- 理解できるまで何度でも繰り返し視聴可能
- 個別最適化された学習プラン
- AIが学習進捗を分析し、最適な学習プランを提案
- 弱点を効率的に克服できるカリキュラム
- モチベーション維持のサポート
- 学習の達成度に応じたポイント制度
- 仲間と競い合える機能で楽しく学習継続
利用者の声
「スタディサプリを使い始めてから、テストの点数が20点以上アップしました！」（中2・女子）
「苦手だった英語が、動画を何度も見て練習問題を解くうちに、だんだん分かるようになってきました。」（中3・男子）
今なら14日間の無料体験実施中！
スタディサプリ中学講座の魅力を、まずは2週間無料で体験してみませんか？
今すぐ登録して、あなたの学習をレベルアップさせましょう！
コメント一覧