【平面図形】おうぎ形の弧の長さと面積の解説動画
本日は中1数学平面図形 おうぎ形の弧の長さと面積について解説していきます。
おうぎ形というだけでよくわからないのに、おうぎ形の弧の長さと面積となるともっとわからないと思う人も多いですよね。
参考書の解説もわかりづらくて勉強が嫌になることもあるのではないでしょうか。
今回は参考書ではありえないくらい丁寧に解説していきます。
前半でおうぎ形の弧の長さと面積について学習してから、練習問題に取り組んでみてください。
おうぎ形の弧の長さと面積について学習
図のように半径をr、中心角をa°、おうぎ形の弧の長さをℓ、扇形の面積をSとすると、
扇形の弧の長さℓは、ℓ =2πr×(a/360)で求めることができます。
こちらの2πrは円周の長さを求める公式になります。円周の長さは直径×円周率で求めることが出来ましたよね。
そして今回、扇形の弧の長さℓを求めるために、円周の長さ2πrにa/360をかけています。こちらどういうことかというと、中心角が円を一周する時の角度が360度になります。この360度のうち今回求めたい扇形の角度は中心角のa°となります。なのでおうぎ形の弧の長さを求めるときは円全体の円周の長さを求めて、それを360で割った上でa倍してあげる。すなわちa/360をかけてあげれば扇形の弧の長さも求めることができます。
次に扇形の面積Sを求めていきましょう。扇形の面積は公式S=πr²×(a/360)で求めることが出来ます。
こちらのπr²は円の面積を求める公式になります。円の面積は半径×半径×円周率で求めることができましたよね。
そして扇形の面積も先ほどの弧の長さと同じように円全体の面積に対して360分の中心角aをかけてあげれば扇形の面積を求めることができます。
なのでおうぎ形の弧の長さと面積の公式は新しく覚えるというよりは円周の長さの公式や円の面積の公式に対して360分の中心角をかけてあげるというふうに覚えておけば大丈夫です。
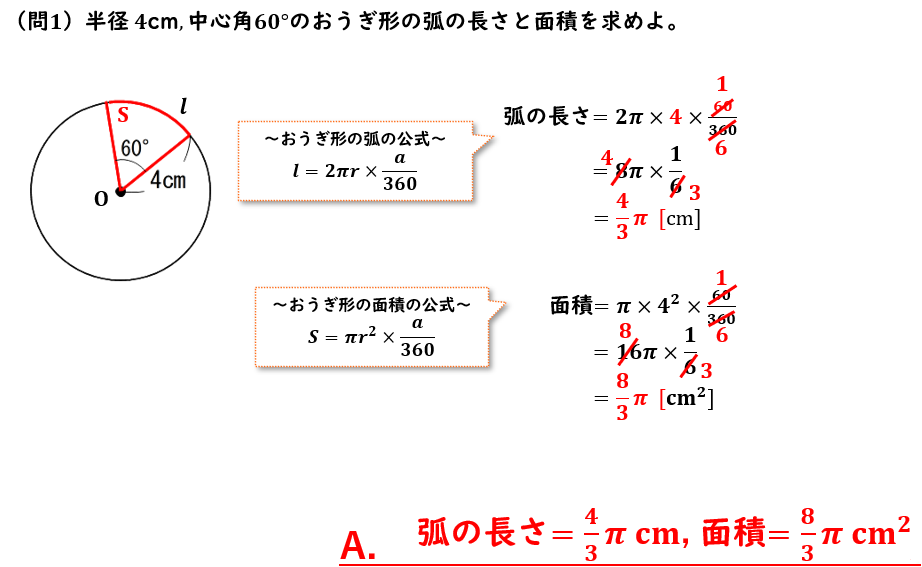
おうぎ形の弧の長さと面積 練習問題 問1
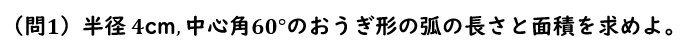
おうぎ形の弧の長さと面積 練習問題 問1 回答と解説
問1の回答
(問1) 回答
弧の長さ (4/3)π cm
面積 (8/3)π cm²
問1の解説
それでは実際に問題を解いていきましょう。
扇形の弧の長さを求める公式はℓ =2πr×(a/360)でしたね。
半径が4 cm、中心角が60°なので式に代入すると、以下のように式を解くことが出来ます。
ℓ =2πr×(a/360)
↓
ℓ =2π×4×(60/360)
↓
ℓ =8π×(1/6)
↓
ℓ =(8/6)π
↓
ℓ =(4/3)π
よって弧の長さは(4/3)π cmであるということが分かりました。
次に扇形の面積の公式を見ていきましょう。公式はS=πr²×(a/360)でしたね。
半径4 cm、中心角60°を代入すると以下のように式を解くことが出来ます。
S=πr²×(a/360)
↓
S=π4²×(60/360)
↓
S=16π×(1/6)
↓
S=(16/6)π
↓
S=(8/3)π
よって面積は(8/3)π cm²であるということが分かりました。
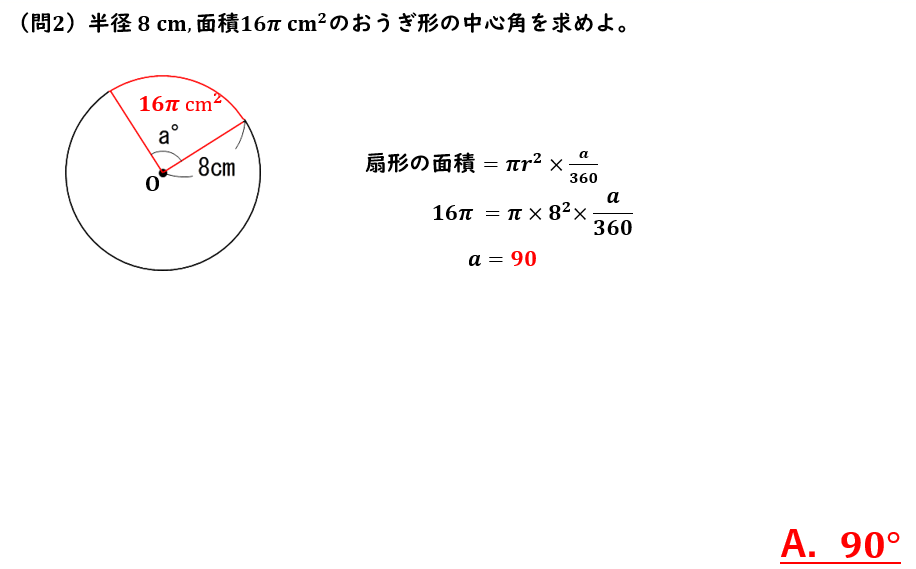
おうぎ形の弧の長さと面積 練習問題 問2
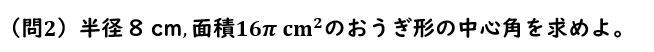
おうぎ形の弧の長さと面積 練習問題 問2 回答と解説
問2の回答
(問2) 回答
90°
問2の解説
今回の問題は先に面積がわかっています。
面積が分かっている上で中心角を求めてくという問題になります。
それでは先ほどと同様に扇形の面積について考えていきましょう。扇形の面積の公式はS=πr²×(a/360)でしたね。
半径が8 cm、面積が16π cm²なので式に代入すると、以下のように式を解くことが出来ます。
S=πr²×(a/360)
↓
16π=π8²×(a/360)
↓（両辺をπで割る）
16=8×8×(a/360)
↓（両辺を16で割る）
1=4×(a/360)
↓（両辺に360をかける）
360=4a
↓
a=90
よって中心角は90°であるということが分かりました。
本日の授業はいかがでしたでしょうか。
関連記事