【空間図形】直線の位置関係(ねじれの位置)の解説動画
本日は中1数学空間図形 直線の位置関係(ねじれの位置)について解説していきます。
直線の位置関係(ねじれの位置)ってよくわからないと思う人も多いですよね。
参考書の解説もわかりづらくて勉強が嫌になることもあるのではないでしょうか。
今回は参考書ではありえないくらい丁寧に解説していきます。
前半で直線の位置関係(ねじれの位置)について学習してから、練習問題に取り組んでみてください。
直線の位置関係(ねじれの位置)について学習
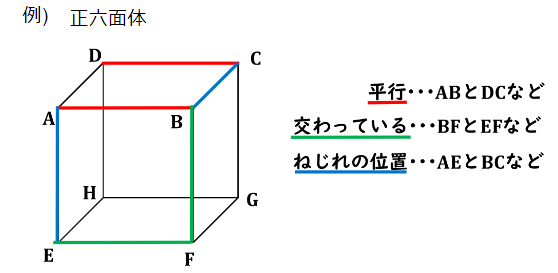
ねじれの位置とは空間内で「交わらず」「並行でないもの」のことを言います。
この説明を聞いてもあまりピンとこないと思うので実際に正六面体をイメージしてみましょう。
まずこれまで習った図形の知識を復習していくと、辺ABと辺DCのように直線をどこまで伸ばしてもその2つの直線が交わらないような関係を「2つの直線が平行である」と表現するのでしたよね。
そして辺BFと辺EFのように、どこかしらの点で辺と辺が交わっている時、その2つの辺は交わっていると言葉のまま表していましたね。
それではねじれの位置はどういった辺と辺の関係性であったかというと、ポイントに記載されている通り「交わらず」「並行でない」辺の関係のことをいいます。
そのため今回のねじれの位置に該当する辺の組み合わせとしては辺AEと辺BCがねじれの位置にあると言えます。
直線の位置関係(ねじれの位置) 練習問題 問1

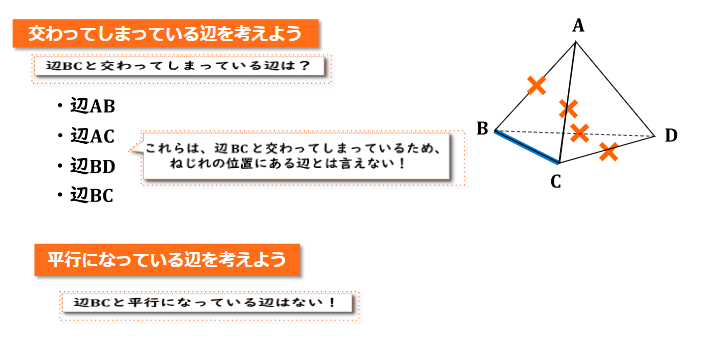
(問1)右の図のような三角錐A-BCDにおいて、辺BCとねじれの位置にある辺はどれか答えなさい。
直線の位置関係(ねじれの位置) 練習問題 問1 回答と解説
直線の位置関係(ねじれの位置) 練習問題 問2
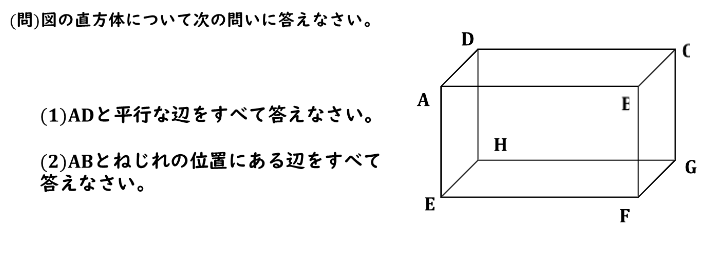
(問2)図の直方体について次の問いに答えなさい。
(1) ADと平行な辺をすべて答えなさい。
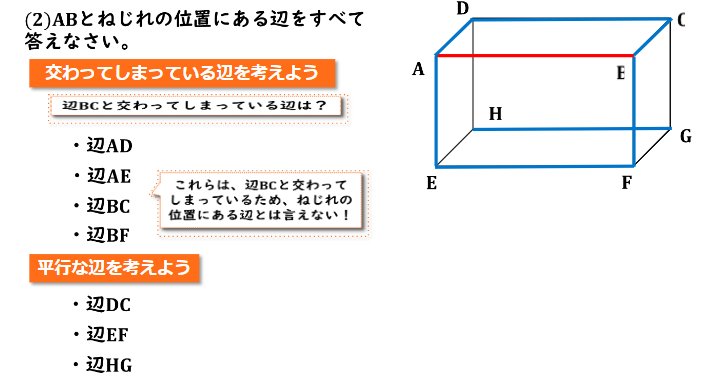
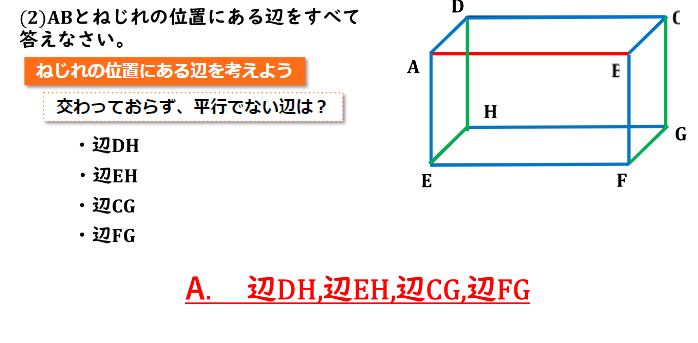
(2) ABとねじれの位置にある辺をすべて答えなさい。
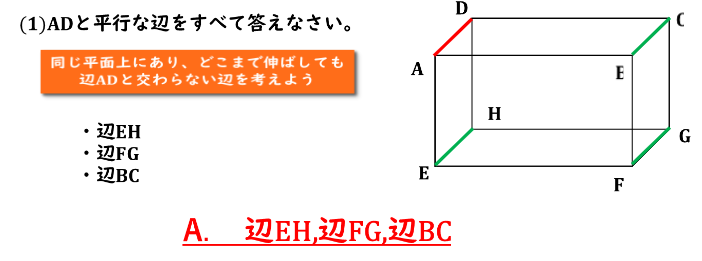
(1) ADと平行な辺をすべて答えなさい。
(2) ABとねじれの位置にある辺をすべて答えなさい。
直線の位置関係(ねじれの位置) 練習問題 問2 回答と解説
本日の授業はいかがでしたでしょうか。














関連記事