【連立方程式の利用】食塩水の文章題 解説動画
本日は中2数学 連立方程式の利用についてやていきます。
についてやっていきたいと思います!
そもそもってなに?って思いますよね
しかも、参考書の解説がわかりづらくて勉強が嫌になるときありますよね
今回の動画では参考書ではありえないくらい丁寧に解説していきますので
高評価&チャンネル登録よろしくお願いします!
それでは本日の問題見ていきましょう。
本日の問題はこちらになります。
解いてみたい方はここで一時停止をしてください。
それでは解いていきましょう!
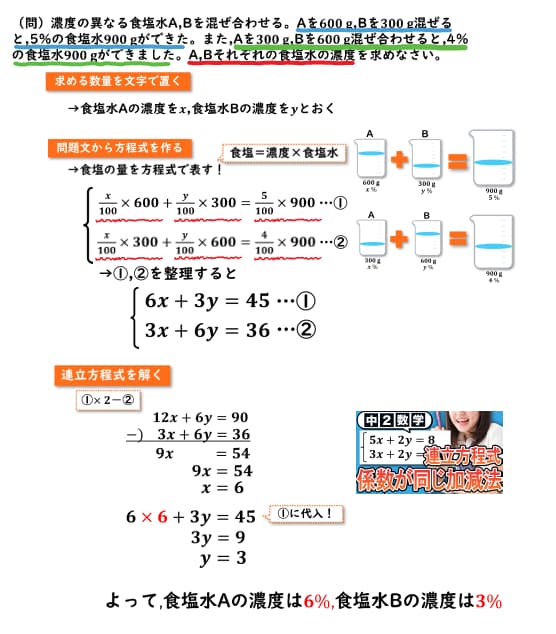
ABそれぞれの食塩水の濃度を求めたいということで、求める数量を文字でおいていきましょう。
食塩水Aの濃度をX、食塩水Bの濃度をYと起きます。
それでは問題文を元に方程式を作っていきましょう。
今回は食塩の量を方程式で表していきましょう。
食塩の量は濃度かける食塩水の量で求めることができます。
それでは問題文を見てみると、まずはAを600g、Bを300gの混ぜると5%との食塩水が900gできたと書いてあるので、
イメージしやすいように図に表すとこのイメージになります。
イメージしやすいように図に表すとこのイメージになります。
こちらを方程式で表してあげると、食塩水Aの濃度を先ほどX%と置いているので、X/100 × 600となります。
また、食塩水Bの濃度もY%と置いているので、食塩水Bの食塩の量はY/100 × 300で求めることができます。これで食塩
水Aと食塩水Bのそれぞれの食塩の量を求めることができました。
こちらを足してあげたのが5%の食塩水900gであると問題文に書いてあるので、5%とは分数に直してあげると、5/100
になるので、5/100 × 900gでおいてあげればOKです。
それではもう一つ同様に見ていきましょう。
問題文を見て分かる通り、Aを300g、Bを600g混ぜ合わせると、4%との食塩水900gができましたと書いてあるので、図に表してイメージしてあげると、このようになります。
それではまず食塩水Aの食塩の量を見ていきましょう。
食塩水Aの濃度はX%なのでX/100 × 300gとなります。
また食塩水Bの濃度はY%なのでY/100 × 600gとなります。
こちらを足したのが、4%の食塩水900gとなっているので、4//4 × 900で求めることができます。
それでは(1)と(2)の二つの式を計算して整理してあげると
(1)の式は6x + 3y = 45、(2)の式は3x + 6y = 36となります。
(1)の式は6x + 3y = 45、(2)の式は3x + 6y = 36となります。
それぞれ分数の計算をしてあげて、約分をしたければOKです。
それでは、この連立方程式を解いて来ましょう。
今回、加減法で解くために(1)の式を2倍してyの係数をそろえてあげました。
なので、引き算で計算してあげると、12x – 3x = 9x、6y – 6y = 0、90 – 36 = 54となり
両辺を9で割ってあげればxの値は6であるということがわかりました。
両辺を9で割ってあげればxの値は6であるということがわかりました。
この値を(1)の式である6x + 3y = 45に代入してあげると、6 × 6 + 3y = 45となります。
計算して移行してあげると、3y = 9となるので両辺を3で割ってあげるとyの値は3であるということがわかりました。
連立方程式の加減法の解き方が分からないよ忘れちゃったよという方は
動画の概要欄の解説動画①をチェックしてみてください。
動画の概要欄の解説動画①をチェックしてみてください。
そちらで詳しく説明をしています。
よってxの値は食塩水Aの濃度であり、yの値は食塩水Bの濃度なので食塩水Aの濃度は6%、
食塩水Bの濃度は3%というのが答えであるということがわかりました。
食塩水Bの濃度は3%というのが答えであるということがわかりました。
本日の授業はいかがでしたでしょうか?
出来た出来ないなどコメントで教えてください。
数学の勉強について悩んでる人向けに公式Lineで質問に答えているので下のボタンから友達追加お願い致します。
Lafの公式LINEで分からない問題が簡単に質問できます!
問題を写真に撮ってチャットで質問できるので解き方が分からない問題があれば気軽に相談してね!
最後まで読んでいただきありがとうございました。















コメント一覧