【確率】サイコロで座標を決めたときの三角形の面積をわかりやすく解説！【中2数学】

 問の回答

問 (1)の解説

まずAとBがどの値になってもいいので、座標平面上に2点A,Bを実際に書いてみましょう。今回は以下の表のようになります。

その上で問題文で問われている線分OAと線分ABの長さについて考えていきましょう。

まず線分OAの長さはaになることは分かるでしょうか。
Aのx座標はa、y座標は0となるのでOAの長さはAのx座標であるaとなりますね。

次にグラフ上の線分ABの長さはbとなることは分かるでしょうか。
点Aと点BのX座標はどちらもaとなっており、線分ABはy軸に平行であるため、Bのy座標から点Aのy 座標を引いた数が線分ABの長さとなりますねよ。なので線分ABの長さはbとなります。

そして今回は線分OAと線分ABの長さの和が10となる確率を求めていきたいので、線分OAの長さaと線分ABの 長さbの和が10となる場合の数を探していくと確率を求めることができます。

ここでa+bが10になる場合の数を考えていくと、
a=4、b=6のとき、
a=5、b=5のとき、
a=6、b=4のとき、
の3通りが挙げられます。

aとbが取る値は1から6までの目があるサイコロなので、aとb は1より小さな値にならず6より大きな値になりませんね。これでa+bが10となる場合の数を求めることができました。

次に確率を求めていくために分母となるすべての組み合わせを考えていきましょう。

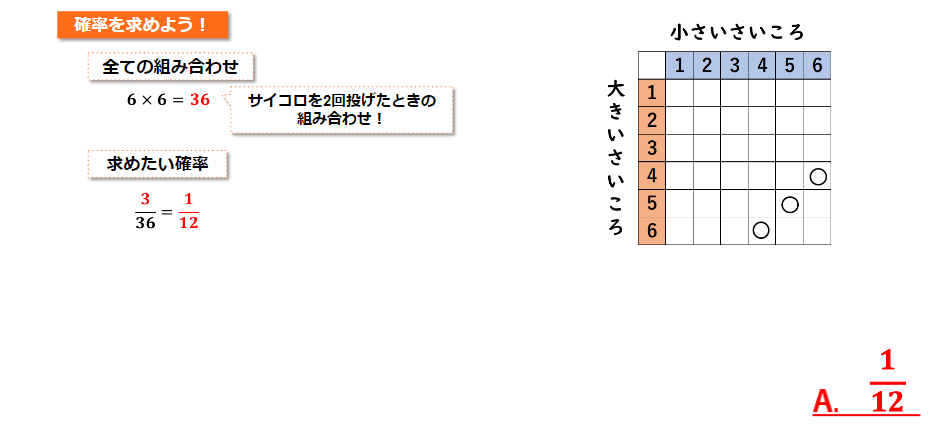
全ての起こり得る場合は、サイコロを2回投げた時の組み合わせなので6×6の36通りですね。
この説明を聞いてあまりピンとこない方は、小さいサイコロと大きいサイコロを投げたときの全ての倍の数を表した表を書いてみるとイメージしやすいかと思います。

線分OAと線分ABの長さの和が10となるのは
大きいサイコロの目が4、小さいサイコロの目が6となる場合、
大きいサイコロの目が5、小さいサイコロの目が5となる場合、
大きいサイコロの目が6、小さいサイコロの目が4となる場合
の3つの組み合わせなので、今回の求めたい確率は36分の3となり、約分して1/12となります。

問 (2)の解説

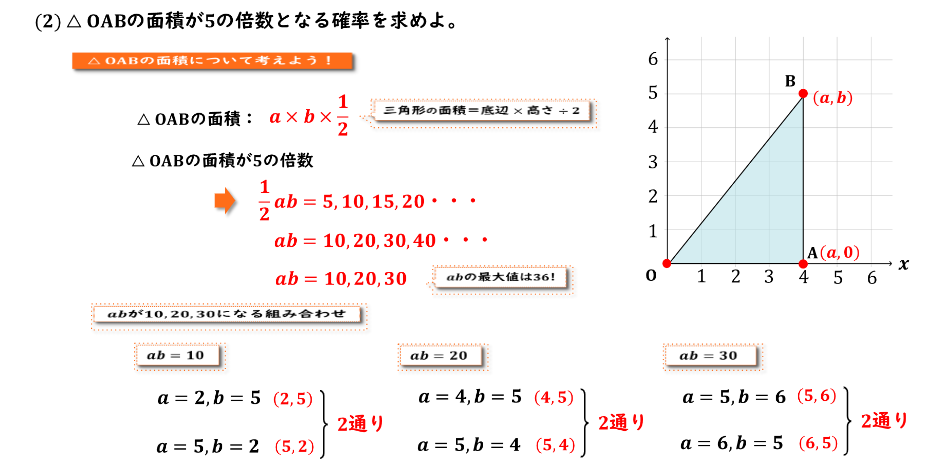
まず△OABの面積をすでに出ている文字式で表すことができるかを考えていきます。

今回はグラフを書いてみると明らかですが、△OABの底辺をOA(=a)、高さをbと考えることができるので、面積はa×b×1/2と表せます。

そして今回は△OABの面積が5の倍数となる確率を求めていきたいので、△OABの面積が5の倍数となる組み合わせを求めていきます。つまり△OABの面積となるa×b×1/2が5,10,15,20といったように5の倍数になっていればいいということです。

そしてこの式の両辺に2をかけていくとa×bが10,20,30,40といったように10の倍数になればいいということは分かるでしょうか。a×b×1/2が5の倍数となるということはa×bが10の倍数になればいいということと同じ意味ですよね。

そしてaとbのとる値の範囲を考えていった時に、aの最大値はサイコロの一番大きな目である6、Bも同様に最大となる値は6となるので、a×bの最大値は6×6で36となります。

よってa×bが30より大きな10の倍数を取ることはありえないので、a×bが10の倍数になるのは10,20,30の3通りしかない、ということになります。

まずa× bが10となるaとbの組み合わせを考えると、
a=2、b=5のとき、
a=5、b=2のとき、
の2通りが考えられます。

この時点で組み合わせの求め方がよくわからないという方は、先ほどの(1)で書いたような36通りの表を書いてみてもいいでしょう。

次にa,bが20となるaとbの組み合わせを考えると、
a=4、b=5のとき、
a=5、b=4のとき、
の2通りが考えられます。

そしてa,bが30となるaとbの組み合わせを考えると、
a=5、b=6のとき、
a=6、b=5のとき、
の2通りが考えられます。

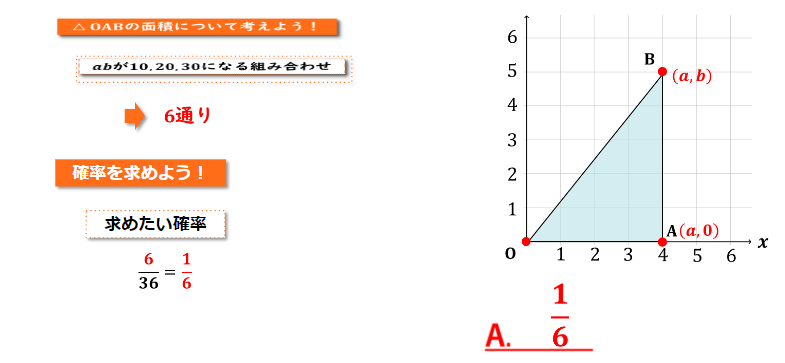
よって△OABの面積を考えた時にa×bが10の倍数（10,20,30）となる組み合わせは合計で6 通りとなります

分母は2つのサイコロを投げた時の全ての起こり得る場合である36通りとなり、分子は a×bが10の倍数となる組み合わせである6通りとなるため36分の6、これを約分して、△OABの面積が5の倍数となる確率は1/6となります。