【確率】樹形図を使った硬貨の問題の解説動画
本日は中2数学確率 樹形図を使った硬貨の問題について解説していきます。
確率の問題は種類が多くてわからない!と思う人も多いですよね。
参考書の解説もわかりづらくて勉強が嫌になることもあるのではないでしょうか。
今回は参考書ではありえないくらい丁寧に解説していきます。
成績アップを目指して練習問題に取り組んでみてください。
樹形図を使った硬貨の問題 練習問題 問1

(問1)2枚の10円硬貨を同時に投げるとき、次の問題を答えなさい。
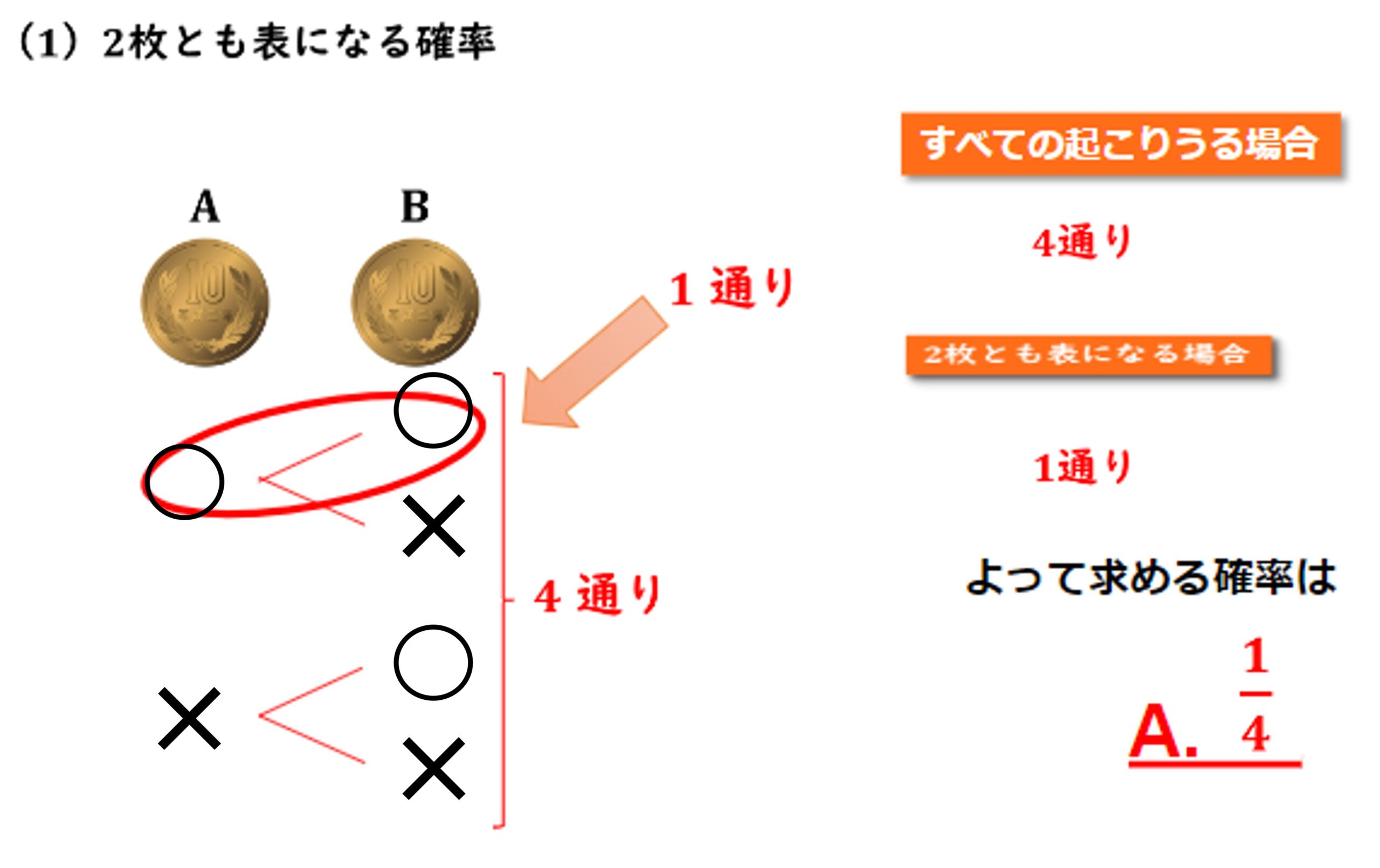
(1) 2枚とも表になる確率
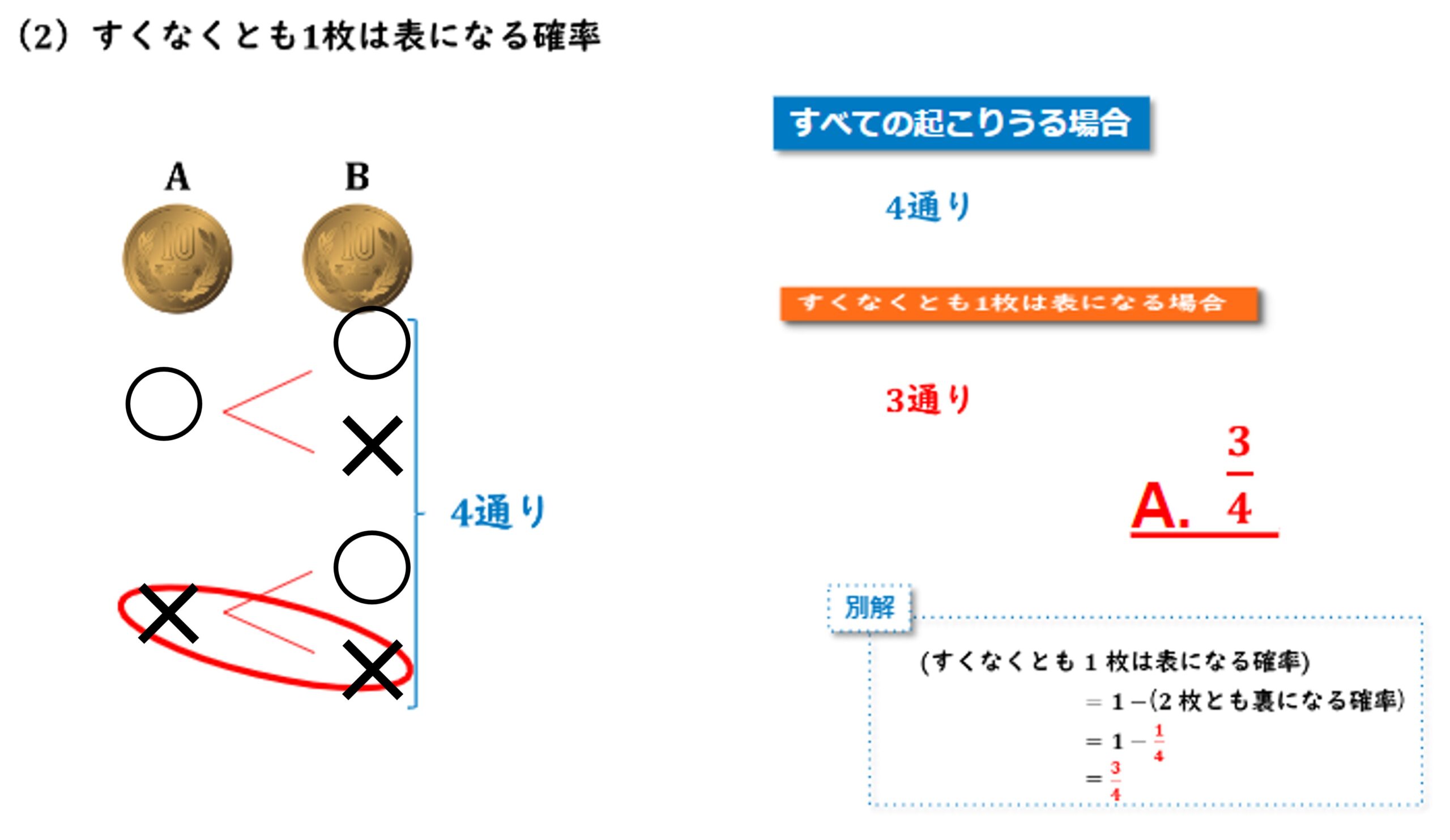
(2) 少なくとも1枚は表になる確率
(1) 2枚とも表になる確率
(2) 少なくとも1枚は表になる確率
樹形図を使った硬貨の問題 練習問題 問1 回答と解説
樹形図を使った硬貨の問題 練習問題 問2

(問2)3枚の10円硬貨を同時に投げるとき、次の問題を答えなさい。
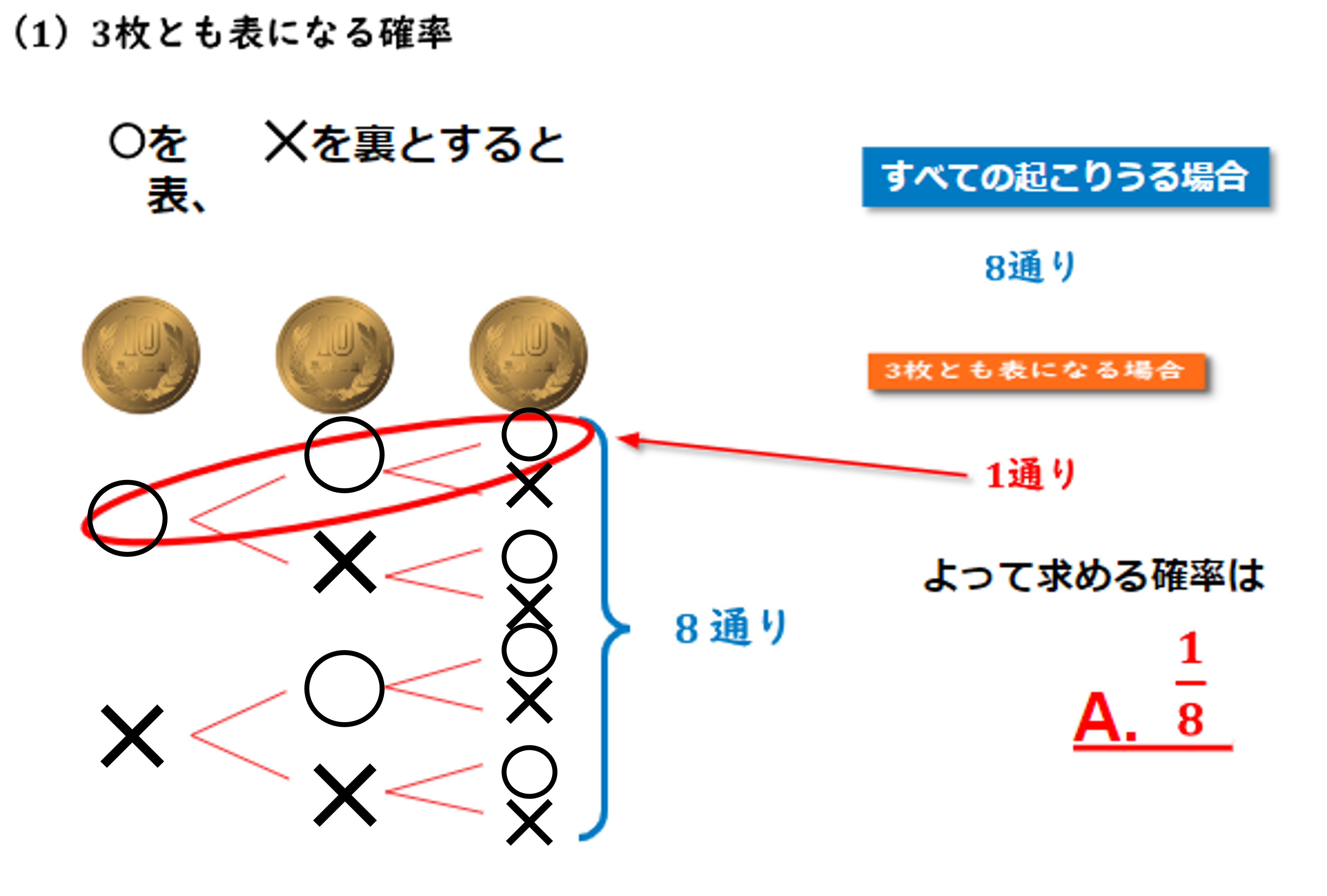
(1) 3枚とも表になる確率
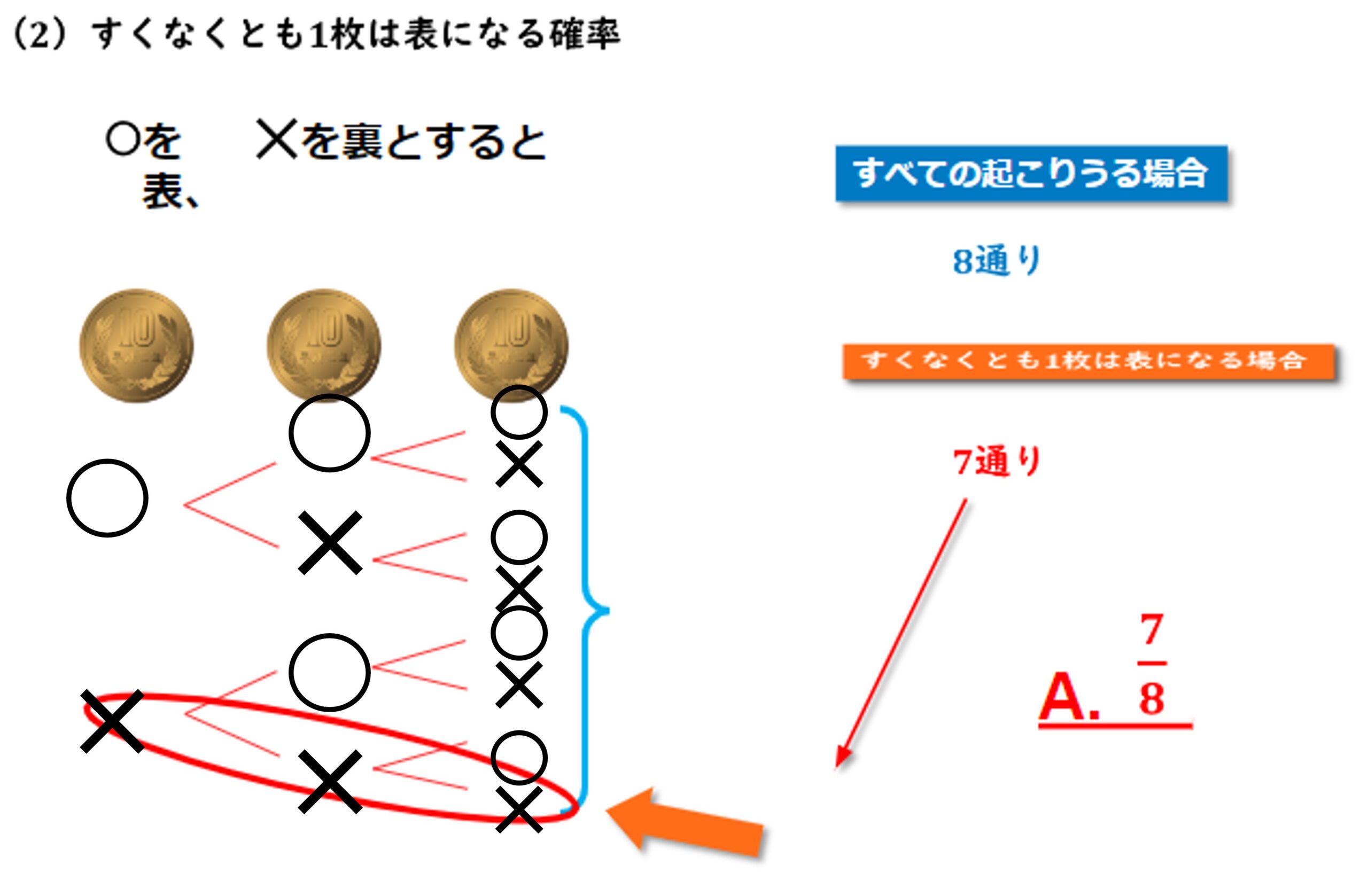
(2) すくなくとも1枚は表になる確率
(1) 3枚とも表になる確率
(2) すくなくとも1枚は表になる確率
樹形図を使った硬貨の問題 練習問題 問2 回答と解説
樹形図を使った硬貨の問題 練習問題 問3

(問3)3枚の10円硬貨を同時に投げるとき、以下の確率を求めなさい。
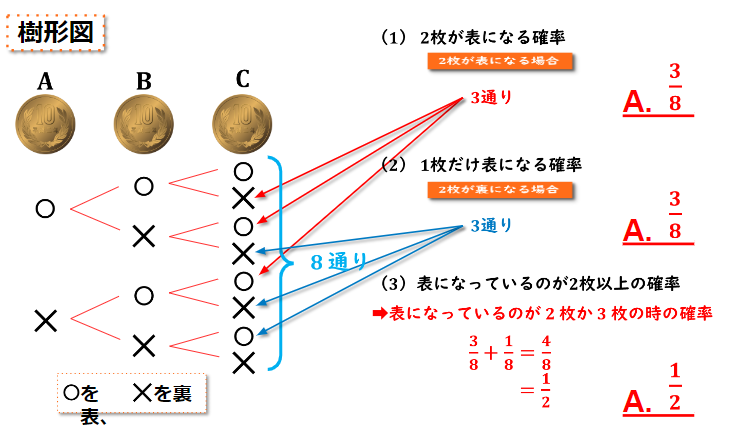
(1) 2枚だけ表になる確率
(2) 1枚だけ表になる確率
(3) 表になっているのが2枚以上あると時の確率
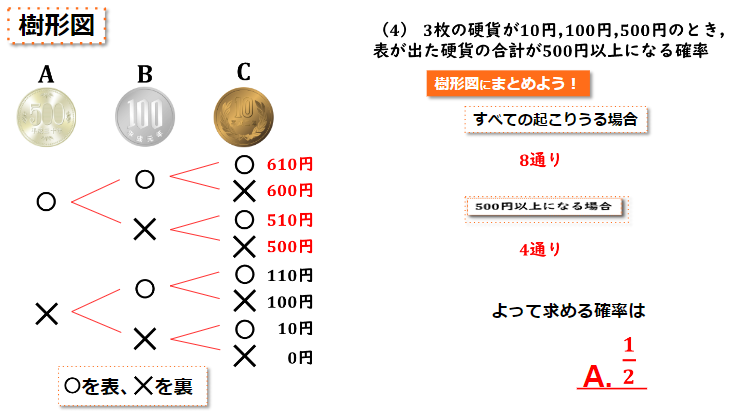
(4) 3枚の効果が10円,100円,500円のとき、表が出た効果の合計が500円以上になる確率
(1) 2枚だけ表になる確率
(2) 1枚だけ表になる確率
(3) 表になっているのが2枚以上あると時の確率
(4) 3枚の効果が10円,100円,500円のとき、表が出た効果の合計が500円以上になる確率
樹形図を使った硬貨の問題 練習問題 問3 回答と解説
樹形図を使った硬貨の問題 練習問題 問4

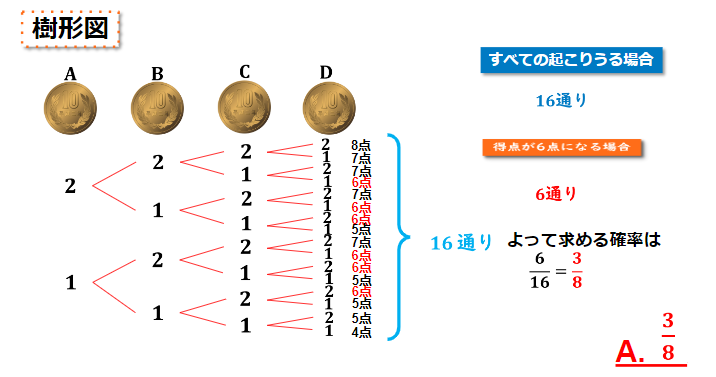
(問4)4枚の硬貨を同時に投げるとき、それぞれの硬貨について、表が出れば2点、裏が出れば1点とし、4枚の硬貨の点数の合計を得点とする。得点が6点となる確率を求めなさい。
樹形図を使った硬貨の問題 練習問題 問4 回答と解説
本日の授業はいかがでしたでしょうか。















関連記事