はい！皆さんこんにちは！
Laf先生です！

本日は中3数学二次方程式
長方形の上を動く点Pと点Qが作る三角形の面積
についてやっていきたいと思います！

そもそも、なんで点を動かすの？？って思いますよね
しかも、参考書の解説がわかりづらくて、勉強が進まないときありますよね

今回の動画では、参考書ではありえないくらい丁寧に解説していきますのでチャンネル登録よろしくお願いします！

ちなみに、動画の最後にテストの予想問題を載せているので確認してみてください！
それでは二次方程式の問題を見ていきましょう！

 

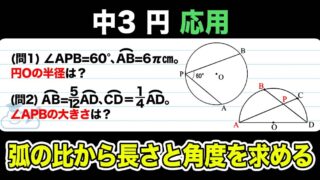
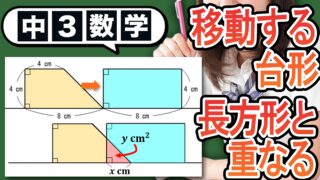
【問題】長方形の上を動く点Pと点Qが作る三角形の面積を求める

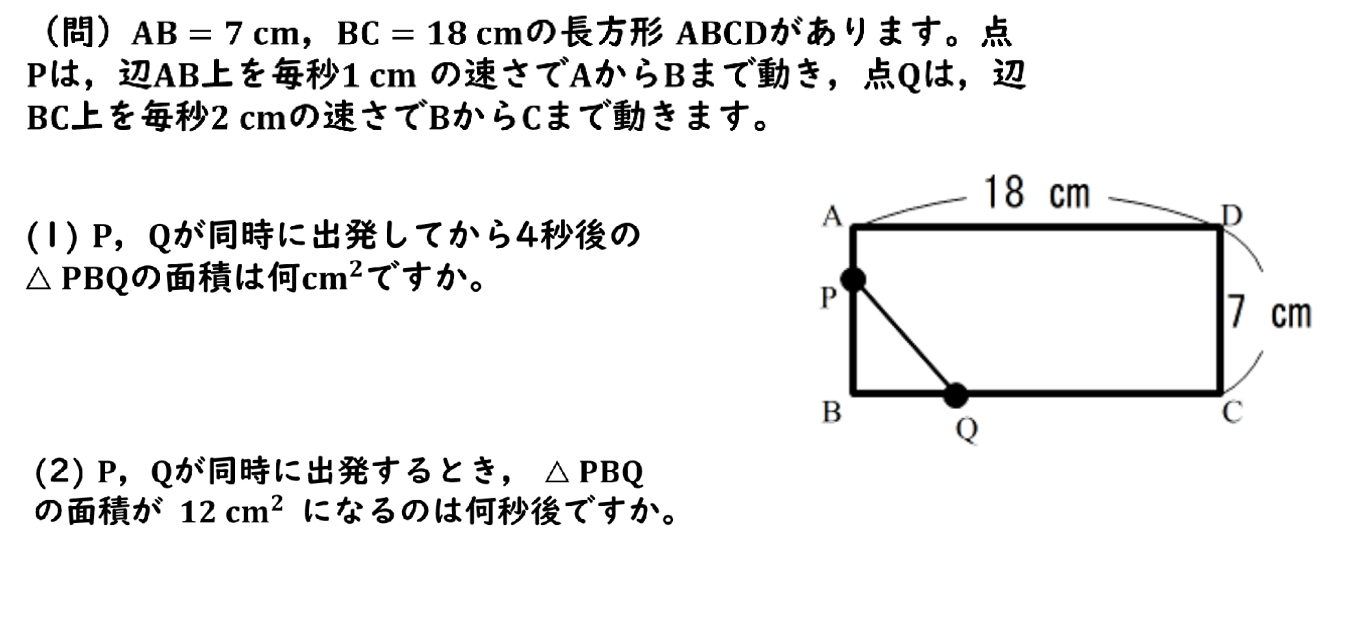
本日の問題はこちらになります！

それでは本日の問題、図に書きながら考えていきましょう！

問題文を読んでわかる通り、点Pは辺AB上にあって、点Qは辺BC上にあります。

そして今回求めたい三角形PBQの面積は、こちらのオレンジ部分になります。

三角形の面積は「底辺×高さ×1/2」で求められるので、PBとBQの長さを求めていきましょう！

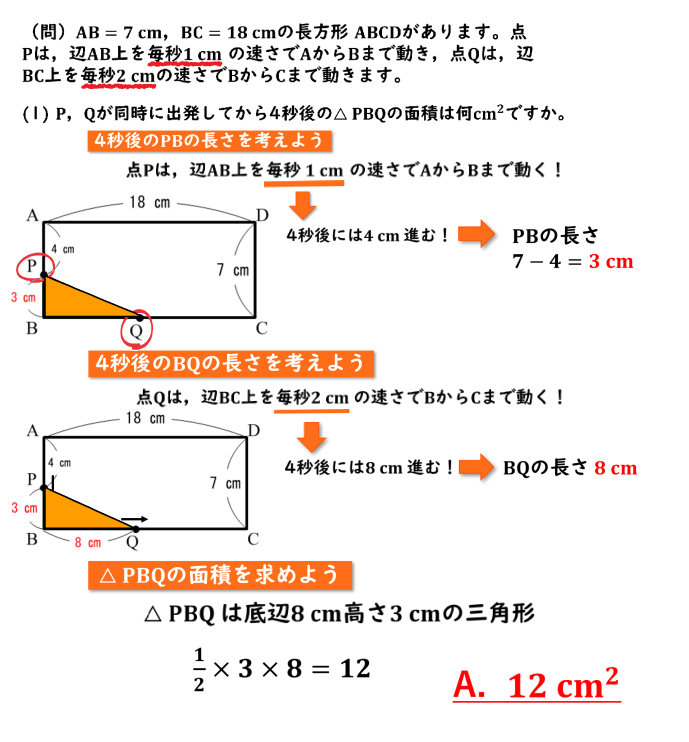
それではまず、4秒後のPBの長さを求めていきましょう。

問題文を見てわかる通り、点Pは辺AB上を毎秒1cm動いているので、4秒後には4cm進んでいることがわかります。
なので、APの長さは4cmであると書き込んであげましょう。

そしてABの長さは7cmなので、PBの長さは7-4で3cmであることがわかりました。

それでは次、4秒後のBQの長さを考えていきましょう。
問題文を見てわかるとおり、点Qは辺BC上に毎秒2cmの速さで動いているということが分かるので、4秒後には8cm進んでいる、ということがわかります。
なのでBQの長さは8cmであると書き込んであげましょう。

それでは三角形PBQの面積を求めてきましょう。
三角形PBQは

• 底辺が8cm
• 高さ3cm

の三角形なので、面積は1/2×3×8で求めることができます。
計算をすると12なので答えは12cm²である、ということはわかりました！

それでは次、

（2）P,Qが同時に出発する時△PBQの面積が12cm²になるのは何秒後ですか？

見ていきましょう！
今回の問題（1）とは逆に、積の大きさが分かっているのですが、秒数がわからないという問題になります。
なので、秒数をx秒後と仮定して問題を解いていきましょう！

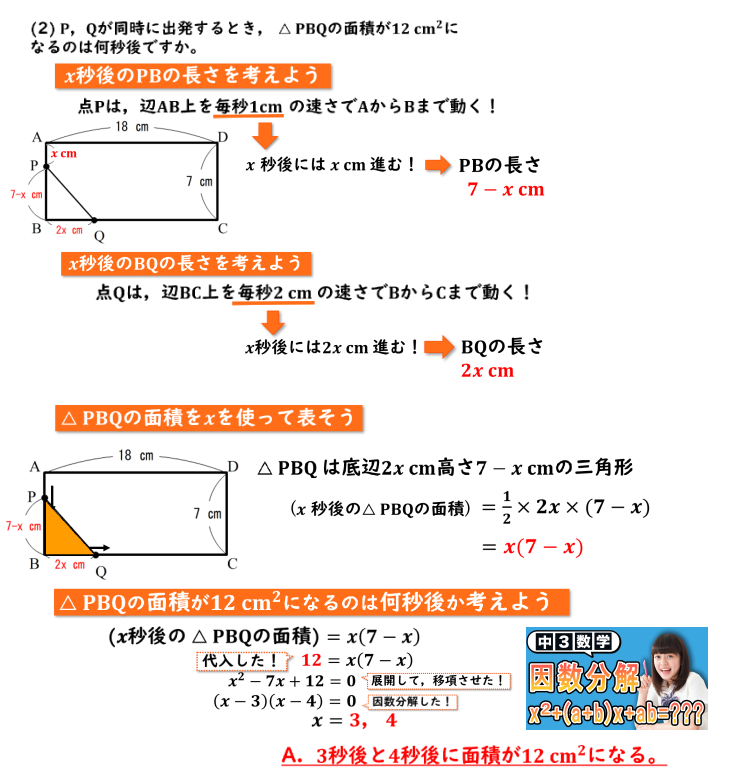
ということで(1)と同様に、x秒後のPBの長さを考えていきましょう！

点Pは辺ABを毎秒1cmの速さでAからBまで動くので、x秒後にはxcm進みます。
なので、APの長さをxcmと書き込んであげましょう。

ABの長さは7cmなので、PBの長さは7-xcmである、ということがわかります！

それでは次、x秒後のBQの長さを考えてきましょう！
点Qは辺BC上を毎秒2cmの速さでBからCまで動いているので、x秒後には2xcm進む、ということがわかります！
なのでBQの長さは2xcmであることがわかります！

それでは三角形PBQの面積をxを使って表していきましょう！
三角形PBQの面積は、こちらのオレンジの三角形になるので、縦の長さは7-xcm、横の長さは2cmであるということがわかります！

 

なので、x秒後の三角形PBQの面積は

1/2×2x×（7-x）

で求めることができます。
計算をしてあげると

x（7-x）

となります。

それでは、三角形PBQの面積が12cm²になるのは何秒後か考えてきましょう！
x秒後の三角形PBQの面積は、先ほど求めた通りx（7-x）となっています。
こちらの面積に12を代入してあげると

x（7-x）＝12

展開して移行させると

x²-7x+12=0

となります。
因数分解をして解いてあげると

x=3,4

xの値は3か4である、ということがわかりました！
今回xは出発してからの秒数を表していたので、今回の問題の答えは3秒ごと4秒後に面積が12cm²になる、ということがわかります！

因数分解の仕方がわからないを忘れちゃったよ！という方は概要欄の解説動画①をチェックしてみてください！

 

 

【練習問題】長方形の上を動く点Pと点Qが作る三角形の面積を求める

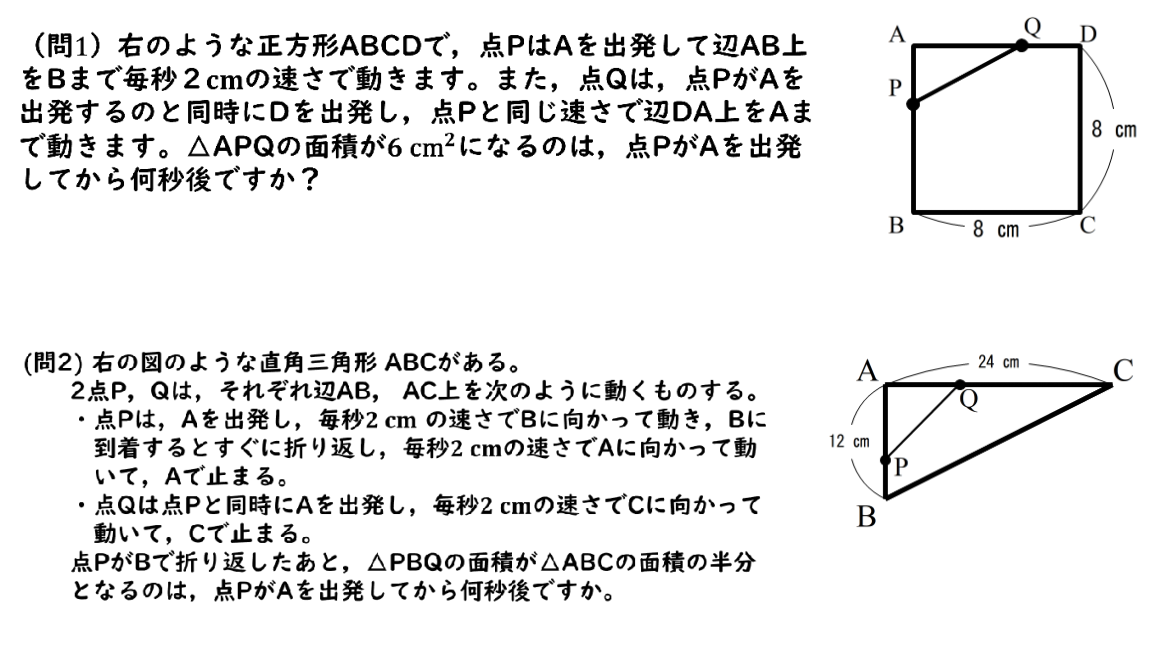
勉強を頑張っている皆さんが、テストで「できる！」ようになるために、テスト予想問題を用意しました！

こちらの公式LINEで解説を見ることができるのでチェックしてみてください！

これからも参考書のざっくりとした解説で困らないように丁寧に解説していきますので、チャンネル登録よろしくお願いいたします！
本日もご視聴ありがとうございました！