【空間図形】球の表面積 解説動画
本日は、中1数学空間図形、球の表面積について行ってきたいと思います。
球の表面積って難しいなって思う人も多いですよね。
しかも参考書の解説がわかりづらくて、勉強が嫌になる時ってありますよね。
今回の動画ではありえないくらい丁寧に解説てきますので、高評価とチャンネル登録よろしくお願いします。
ちなみに動画の最後にテスト予想問題を載せているので、チャレンジしてみてください。
それでは本日の問題を見てい行きましょう!
本日の問題はこちらになります!
球の表面積を求める様々なパターンを用意してみました。
自力で解いてみたい方は、ここで一時停止をしてください。
では解いていきましょう!
それでは、本日の問題文を見てわかる通り表面積の計算になります。
本日のポイント
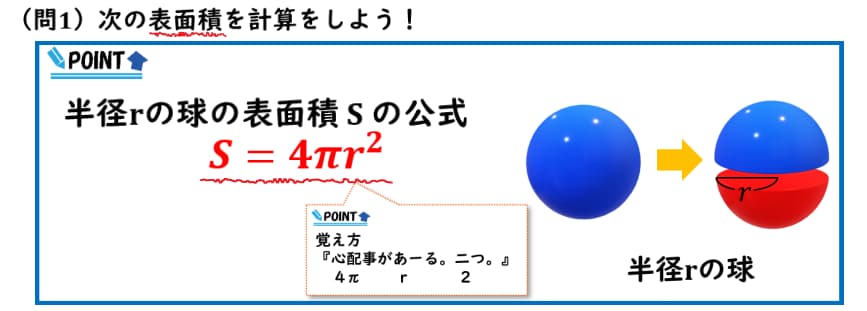
πr²は円の面積を求める公式でしたが、4倍すると球の表面積となります。S = 4 πr²こちらをしっかり覚えておきましょう。
こう言われても、すんなり覚えるのが難しいと思いますので
一つだけ、語呂合わせで覚えるやり方も共有しておきます。
語呂合わせはこちらになります
「心配事がある二つ」
これで4パイアール二乗と覚えておきましょう。
それではこちらの公式を使って本日の問題を解いていきましょう。

(1)半径2cmの球、こちらの表面積見ていきましょう。
公式より球の表面積は4πr²で求めることができるので
こちらのrは半径の2cmなので2を代入してあげると
4π × 2² となります。
2²は4なので計算をしてあげると16π cm² が今回の球の表面積であるということがわかりました。
こちらがいまいちよく分からなかったよという方は公式Lineに質問かコメント欄に投稿お願いします。

それでは次、(2)直径8cmの球、見ていきましょう
直径が8cmの球ということは、半径の大きさは直径の半分なので、8 × 1/2 で4cmであるということが分かります。
なので今回、求めたい球は半径が4cmの球となります。
それでは公式よりきゅーの表面積は4πr²のrに4を代入してあげればよいので
4π × 4²となり計算をしてあげると、64cm² であるということがわかりました。
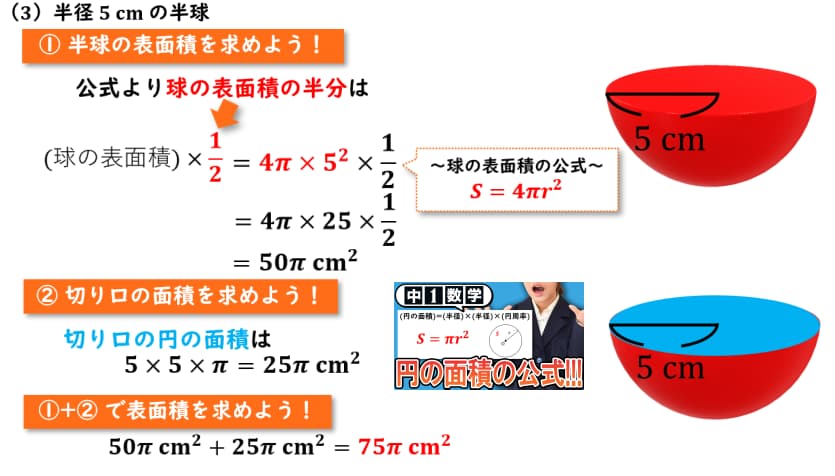
それでは次、(3)半径が5cmの半球、見ていきましょう。
それでは、今回の半径5cmの半球とはこちらの図の様になります。
半球とは、球を真っ二つにして半分にしたものです。
それではまずこちらの半球の球の部分の表面積を求めていきましょう。
公式より、球の表面積の半分は球の表面積を1/2してあげれば、求めることが出来ます。
半分なので1/2するのは当たり前ですよね。
それでは球の表面積を代入してあげるとこのようになります。
球の表面積の公式はS =4πr² だったので今回は半径5cmなのでrの部分に5を代入してあげると4π × 5² となります
計算をしてあげると50π cm² であるということが分かりました。
それでは次、切り口の面積を求めていきましょう。
今回の半球の表面積を聞かれている場合、こちらの図のように青い部分の切り口の面積も求めないといけません。
こちらを求めず、球の部分の表面積だけを答えに書く人がめちゃくちゃ多いので、
皆さんも同じような間違いはしないように気をつけてください。
それでは、この切り口の部分は円の面積になりますので、円の面積の公式は、半径 × 半径 × 円周率 なので
こちらの方程式のようになります。
半径が5cmなので、5 × 5 × π、計算すると25π cm² となります。
円の面積を求める公式がわからない、忘れちゃったよという中学生は
概要欄の解説解説動画①をチェックしてみてください。
そちらで丁寧に解説をしています。
それでは、①で求めた球の部分の表面積と②で求めた切り口の部分の面積を足して表面積を求めていきましょう。
ということで50π cm²と25π cm² を足してあげると75π cm² となります。
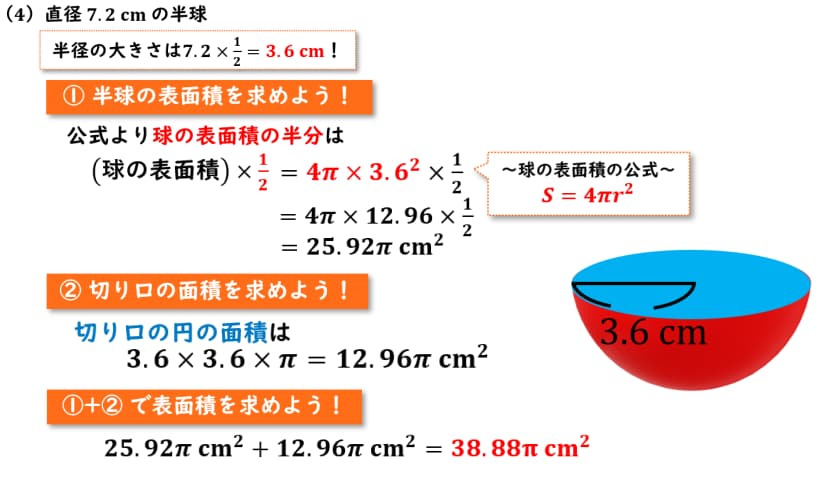
それでは次、直径が7.2cmの半球を見ていきましょう。
こちらも直径が7.2cmなので半径の大きさは7.2cmを1/2倍してあげれば求めることができるので
計算をしてあげると半径の値は3.6cmであるということがわかります。
半径が3.6cmの半球はこちらの図のようになります。
それでは、先ほど同様に半球の球の部分の表面積を求めていきましょう。
公式より球の表面積の半分は球の表面積 × 1/2 で求めることができて
球の表面積を代入してあげるとこちらの方程式の様にになります。
球の表面積の公式はS = 4πr² でしたね今回、半径が3.6cmなのでrの部分に3.6を代入してあげましょう。
計算をすると25.92π cm² であることが分かりました。
それでは次、切り口の円の面積を求めていきましょう。
こちらの円の面積は3.6 × 3.6 × π で求めることができます。
円の面積の公式は半径 × 半径 × 円周率で求めることができましたね。
こちらを計算してあげると12.96π cm² であるということが分かりました。
それでは、①で求めた球の部分の表面積と
②で求めためた切り口の部分の面積を足してあげると答えは、38.88 cm²であるということがわかりました。
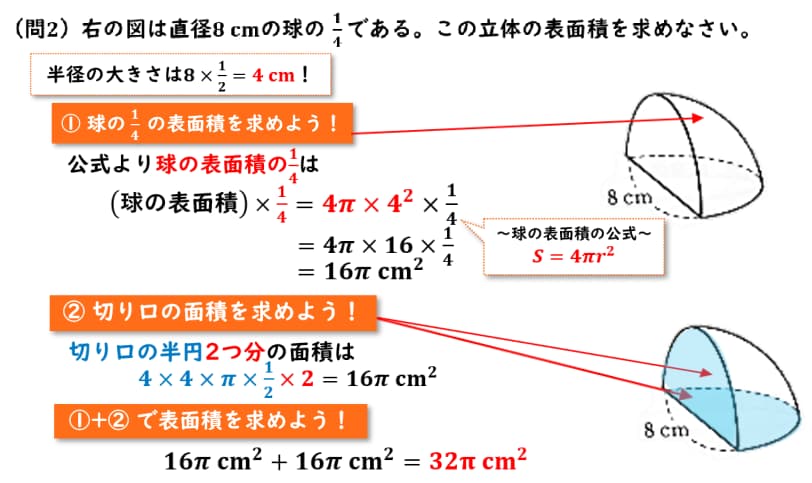
それでは最後、問2。
右の図は直径8cmの球の1/4である。この立体の表面積を求めなさい。
今回の球は直径が8cmなので半径の大きさは8 × 1/2で求めることができます。
なので半径の大きさは4cmであることがわかりました。
それでは、この1/4した球の部分の面積を求めていきましょう。
公式より球の表面積の1/4は、球の表面積 × 1/4で求めることができます。
なので今日の表面積の部分に代入してあげるとこのようになります。
球の表面積の公式はS = 4πr²なのでrの部分に4cmを代入すると4π × 4² となります。
計算をすると16π cm² であるということがわかりました。
それでは次、切り口の面積を求めていきましょう。
今回、気をつけて欲しいのは切り口が二つあることです。
一つ目はこちらの底面でありもう一つはこちらの側面の半円になります。
なので切り口の半円二つ分なので円の面積の公式は半径 ×半径 × 円周率なので方程式を立てると、このようになります
4 × 4 × πで円の面積を求めていて、そちらの半分にしなくてはいけないので
1/2倍してあげてこちらのの半円が二つあるので、2倍してあげるというふうになります。
計算をしてあげると、16π cm² であるということがわかりました。
こちらが、いまいちよく分からなかったよという方は公式Lineに質問かコメント欄に投稿お願いいたします。
それでは、この一つ目で求めた球の部分の表面積と切り口の部分の表面積を足してあげると
16π cm²と16π cm²を足してあげればいいので32π cm²が今回求め球を1/4した表面積となります。
本日の授業はいかがでしたでしょうか?
出来た出来ないなどコメントで教えてください。
数学の勉強について悩んでる人向けに公式Lineで質問に答えているので下のボタンから友達追加お願い致します。
Lafの公式LINEで分からない問題が簡単に質問できます!
問題を写真に撮ってチャットで質問できるので解き方が分からない問題があれば気軽に相談してね!
勉強を頑張っている皆さんが「テストでできる!」ようになるためにテスト予想問題を用意しました。

こちらも公式LINEで解説を見ることができるのでチェックしてみてください。
最後まで読んでいただきありがとうございました。


















コメント一覧