【平面図形】平行移動してできる図形をわかりやすく解説！【中1数学】

【平面図形】平行移動してできる図形の解説動画
平行移動について学習
平行移動してできる図形練習問題問1
平行移動してできる図形練習問題問1 回答と解説
平行移動してできる図形練習問題問2
平行移動してできる図形練習問題問2 回答と解説

「話題沸騰中！16大メディアが注目したLaf先生AI – あなたの学びをもっと身近に」

各社が報じた話題のAI教育ツール。24時間質問し放題、理解度に応じた解説で、わからないをゼロに。今すぐ試して、学びを加速させよう。

※様々なメディア様に注目いただき、反響多数！現在TV取材も予定している注目サービスとなっています。（一部掲載）

【平面図形】平行移動してできる図形の解説動画

本日は中1数学平面図形平行移動してできる図形行について解説していきます。

平行移動は数学において基礎的な知識です。

しかし参考書の解説もわかりづらくて勉強が嫌になることもあるのではないでしょうか。

今回は参考書ではありえないくらい丁寧に解説していきます。

前半でしっかりと基礎的な知識を確認したら、後半の練習問題を解いてみましょう。

平行移動について学習

まず問題を解いていく前に、今回新しく出てくる用語「平行移動」について解説していきます。

平行移動とは、図形を一定の向きに一定の距離だけ移動することを言います。

この平行移動の特徴として、平行移動した図形と対応する点を結んだ線はすべて平行であり、それらの線分の長さは全て等しくなっています。

たとえば下の三角形ABCをみると、三角形ABCを平行移動した先にできた図形が三角形A’B’C’となります。この2つの三角形を見ていった時に、平行移動した図形と対応する点はAとA’、BとB’、CとC’になっているので、線分AA’と線分BB’と線分CC’は全て平行となります。

また平行移動した図形と対応する点を結んだ線分の長さは全て等しいので、線分AA’=線分BB’=線分CC’となります。

対応する点を結んだ線分がすべて平行かつ長さが等しいという平行移動の性質は平行移動を議論する上でかなり重要となるので、ここでしっかりと覚えておきましょう。

平行移動してできる図形練習問題問1

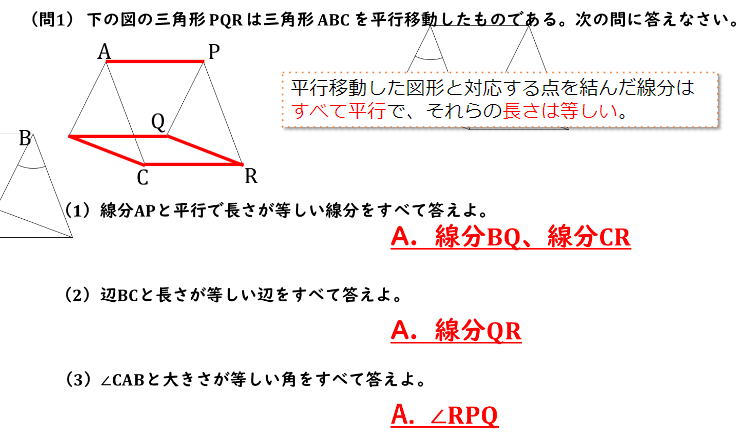
（問1）下の図の三角形PQRは三角形ABCを平行移動したものである。次の問に答えなさい。
(1) 線分APと並行で長さが等しい線分をすべて答えよ。
(2) 辺BCと長さが等しい辺をすべて答えよ。
(3) ∠CABと大きさが等しい角をすべて答えよ。

平行移動してできる図形練習問題問1 回答と解説

クリックで回答と解説を見る

問1の回答

(問1) 回答
(1) 線分BQ、線分CR
(2) 線分QR
(3) ∠RPQ

問1 (1)の解説

前半では平行移動した図形と対応する点を結んだ線分は平行で長さが等しいことを確認しましたよね。

今回問われている線分APは平行移動した図形と対応する点を結んだ線分となっているので、同様に対応する点を結んだ残りの線分を探していけば、その線分が平行で長さが等しいということになります。

よって三角形PQRのうち点Pは点Aに対応しているので、残りの点Qと点Rに着目していきましょう。

点Qは点Bに対応しているため、平行移動した図形と対応する点を結んだ線分はBQとなります。

同様に点Rも点Cに対応しているので、平行移動した図形と対応する点を結んだ線分はCRとなります。

よって線分APと平行で長さが等しい線分は線分BQと線分CRの2つとなります。

問1 (2)の解説

三角形PQRを一定の向きに移動した時の図形が三角形ABCとなっていることが分かります。

よって平行移動する前のPQRとABCは合同であるということがわかります。つまり対応する辺が等しいということになります。

三角形PQRを見ていくと、辺BCに対応する辺は辺QRのみとなっているので、辺BCと長さが等しい辺は線分QRとなります。

問1 (3)の解説

三角形PQRを一定の向きに移動した時の図形が三角形ABCとなっているので、三角形PQRと三角形ABCは合同でしたよね。よって∠CABに対応する∠を三角形PQRから見つけることができれば、その角が∠CABと大きさが等しい角ということになります。

今回は∠CABに対応する角は∠RPQであることが言えますね。したがって∠CABと大きさが等しい角は∠RPQであることが分かりました。

先ほど三角形ABCと三角形PQRが合同であるという用語を用いたと思いますが、「合同」のことはまだ習っていない方が多いと思います。現段階では「合同」というのは「2つの図形を重ねた時に2つの図形がぴったり重なる」という解釈で大丈夫です。詳しくは中2の数学で「合同」について学習していくので、今回は平行移動する前の図形はぴったり重なるというイメージを持っておきましょう。

平行移動してできる図形練習問題問2

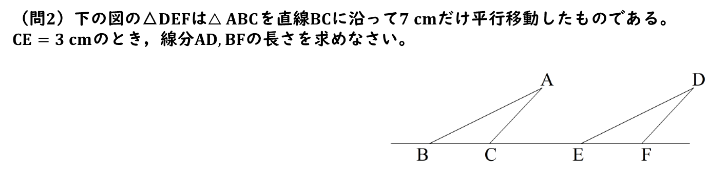
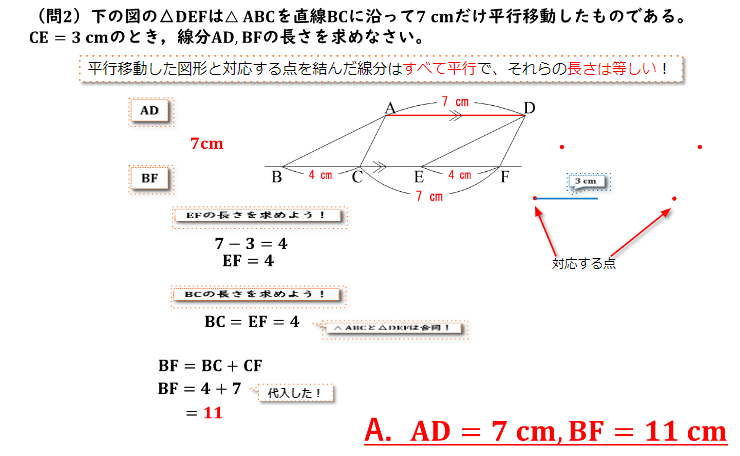
（問2）下の図の△DEFは△ABCを直線BCに沿って7cmだけ平行移動したものである。CE=3cmのとき、線分AD、BFの長さを求めなさい。

平行移動してできる図形練習問題問2 回答と解説

クリックで回答と解説を見る

問2の回答

(問2) 回答
AD=7cm、BF=11cm

問2の解説

三角形ABCがBCに沿って7cm平行移動したものが三角形DEFとなります

よってAから7cm移動した時の点が点Dとなるため、線分ADの長さは7cmであることがわかります。

線分BFの長さを求めていく上でまずは線分EFの長さを求めていきましょう。まず図でもすでに記載されていますが線分CFの長さが線分ADと同じ7cmであることは分かるでしょうか。平行移動した図形と対応する点を結んだ線分の長さはすべて等しいんでしたよね。よって線分CFの長さは7cmであることがわかります。

そして問題文の条件にCE=3cmであるという記載があることも確認しておきましょう。そうすると線分EFの長さは線分CFの長さからCEの長さを引いた数であるということは分かるでしょうか。

よって線分FCの長さである7cmから線分CEの長さである3cmを引いたEFの長さは4cmであるということが言えます。

次に線分BCとそれに対応する線分EFの長さは同じとなっているので、BC=EF=4cmであることが言えます。

よって今回問題に問われている線分BFの長さは、右の図から線分BCの長さと線分Cその長さの和であるので、線分BFの長さは4cm+7cm、つまり11cmであることが分かりました。

平行移動について覚えるべきポイントは図形と対応する点を結んだ線分が全て平行、そして長さが等しくなるといったポイントと、平行移動をする前とした後の2つの図形はぴったり重ねることができるという2つのポイントをしっかりと覚えておきましょう。