【二次関数】二次関数の最小値・最大値・変域 解説動画
本日は中3数学 二次関数二次関数の最小値・最大値・変域についてやっていきたいと思います!
そもそも変域とか言われても、よく分からないと思う人も多いですよね
参考書の解説もわかりづらくて勉強が嫌になることもあるのではないでしょうか。
今回は参考書ではありえないくらい丁寧に解説していきます。
ちなみに、動画の最後にテスト予想問題を載せているので、チャレンジしてみてください!
それでは二次関数の問題見ていきましょう!
二次関数の最小値・最大値・変域の問題

それでは解いていきましょう!
二次関数の最小値・最大値・変域の解説(1)
まず、変域の問題を考える時はざっくりとでいいので、グラフを書きながら考えていきましょう。
頭の中で考えるとごちゃごちゃしてわかりづらいです!
今回の問題はy=(1/4)x²なので、グラフに書いてあげるとこのような形になります。
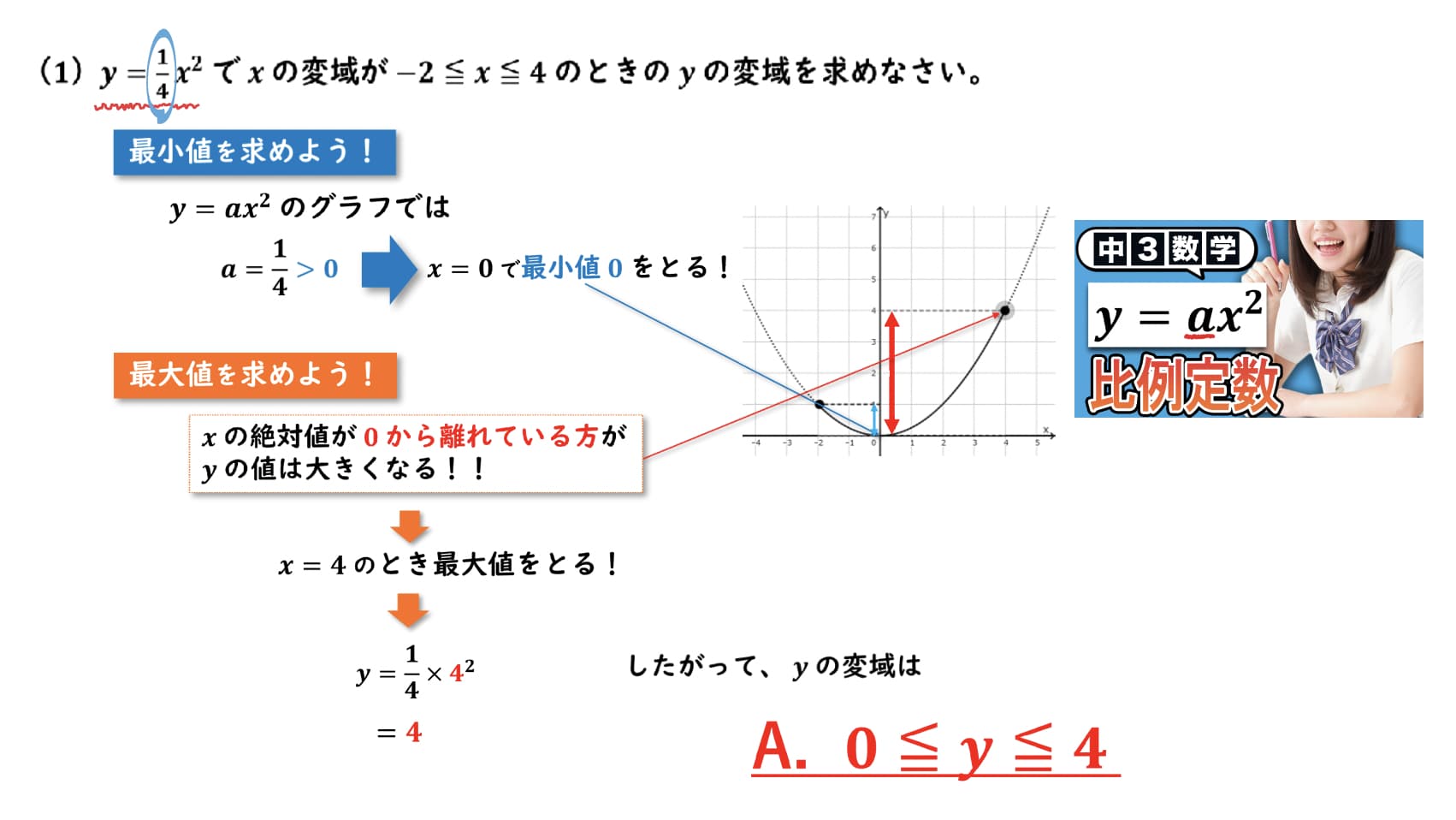
そして、今回の二次関数の比例定数は1/4となり、0より大きいことがわかります。
比例定数について分からないよ、忘れちゃったよーという方は、概要欄の解説動画1をチェックしてみてください!
それでは、比例定数が0より大きくなる時の二次関数の特徴について説明していきたいと思います。
本日のポイント
比例定数が0より大きい時の特徴は3つあります!
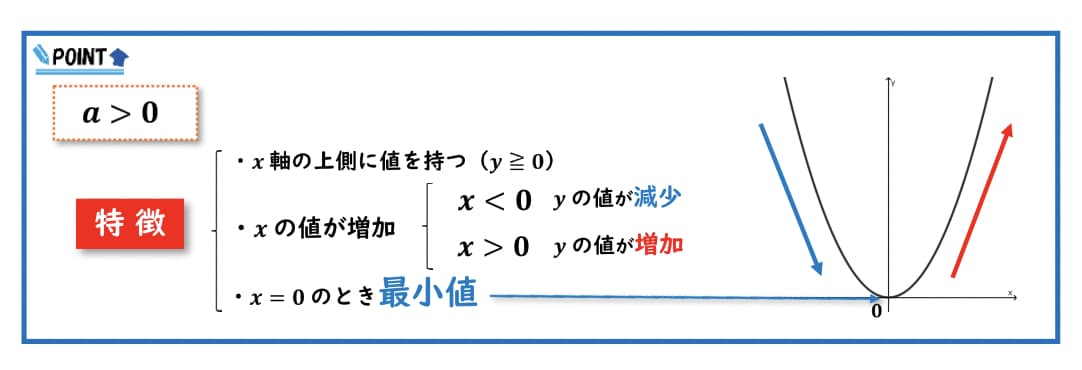
x軸の上側に値を持ちます
x軸より下側には値を取りません。
こちらのグラフのように、x軸より上に値をとります。
下に値を取ることはありません。
xの値が増加していくとき、xの値が0より小さいときはyの値はこのように減少していきます。
そして、xの値が0より大きいときは、yの値は増加していきます。
このようにyの値は減少して増加する、というのが比例定数aが0より大きい時のグラフの特徴です。
x=0のとき最小値をとります。
このように原点を通る時、グラフのようにxが0のとき、yの値が一番小さくなることがわかります。
それでは実際に問題を解きながら説明していきます。
まずは最小値を求めていきましょう!
今回、二次関数y=ax^2のグラフでは、aの値が1/4なので0より大きいことがわかります。
なので、x=0で最小値0を取るということがわかります。
では次、最大値を求めていきましょう!
最大値はxの絶対値が0から離れている方が、どんどんyの値が大きくなるということがわかります。
グラフを見てわかる通り、xが-2のときのyの値より、xが4のときのyの値の方が、大きくなっているということがわかります。
なので、比例定数aが0より大きいグラフでは、xの絶対値が0から離れていればいるほど値が大きくなる、ということを覚えておきましょう!
なので、今回の最大値は、x=4のとき取るということがわかります。
よって、y=1/4x^2のxに4を代入してあげて、計算をすると4であるということが分かりました。
したがって、yの変域は0以上4以下である、ということがわかりました。
二次関数の最小値・最大値・変域の解説(2)

見ていきましょう!
まず今回の問題の特徴は、xの変域とyの変域が分かっているので、こちらの二つの要素を使ってaの値を求めていく、というのが今回の問題になります。
それでは今回もグラフに書いて考えていきましょう!
グラフに書くとこのようになります。
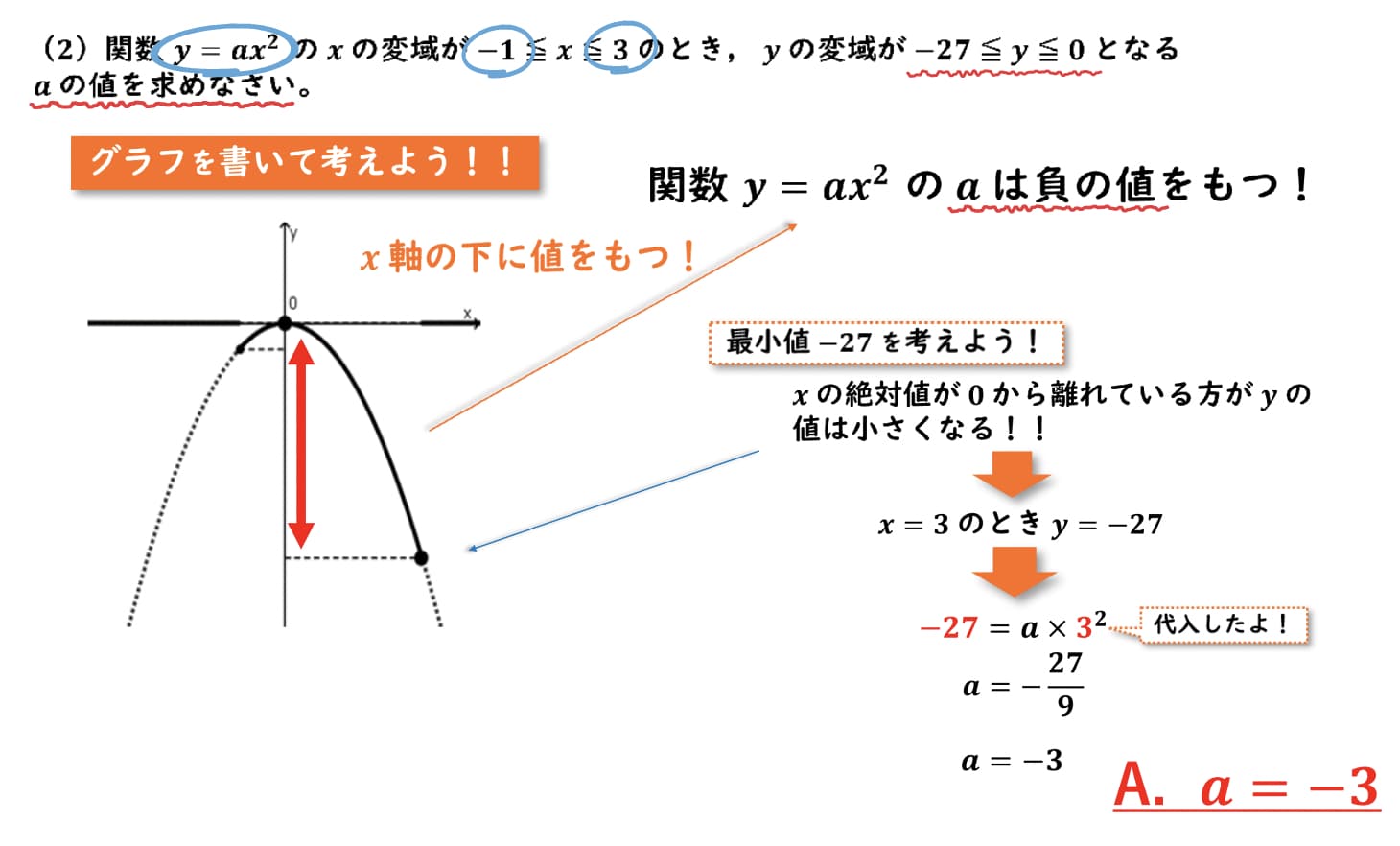
yの変域が-27から0なので、yの値は負の値をとるということがわかります。
なので、二次関数のグラフは下に開くグラフを書いてあげましょう。
よって、x軸の下に値を持つことが分かるので、関数y=ax^2のaは負の値を持つ、ということがわかります。
それでは、比例定数aが負の値を持つときのポイントを説明してきたいと思います。
比例定数aが0より小さい時の特徴は3つあります!
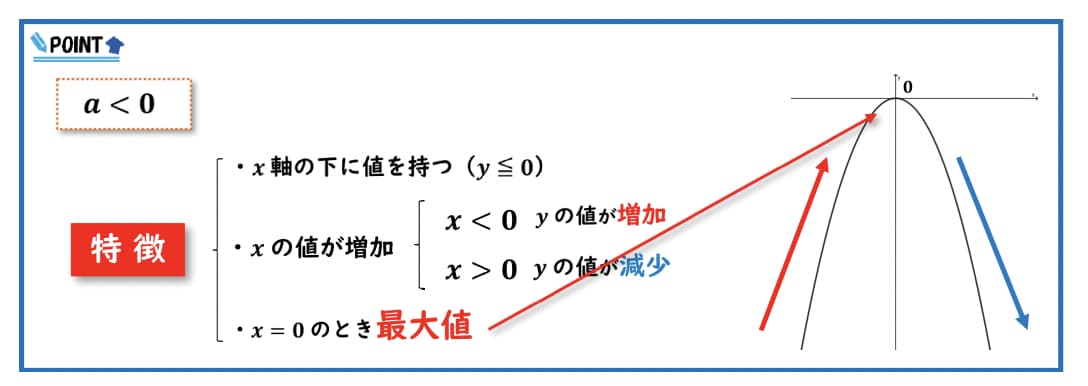
1つ目:x軸の下に値を持ちます
グラフのように下に開くグラフになります。
そして2つ目:
xの値が増加しているとき、xが0より小さいときはyの値は増加していき、xが0より大きくなったらyの値は減少していく
ということがわかります!
そして3つ目:xの値が0のとき最大値を取る、というのが比例定数aが負のときのグラフの特徴になります!
それではこちらの3つの特徴を踏まえた上で問題を解いていきましょう!
まず今回のyの最小値-27について考えていきましょう。
グラフを見てわかる通り、比例定数aがマイナスの場合、xの絶対値が0から離れている方がyの値はどんどん小さくなっていきます。
今回、xの変域は-1以上3以下であり、-1の絶対値は1、3の絶対値は3なので、xが3のときの方が0から離れているということがわかります。
なので、xが3のときyの最小値である-27を取る、ということがわかります。
今回の二次関数であるy=ax^2に代入してあげると、yの値が-27、xが3なので、-27=a×3²となります。
計算をしてあげると、aの値が-3であるということがわかりました。
よって、答えはa=-3となります!
二次関数の最小値・最大値・変域の練習問題
本日の授業はいかがでしたでしょうか?
数学の勉強について悩んでる人向けに、公式LINEで質問に答えているので、こちらから友達追加お願い致します!

勉強を頑張っている皆さんが、テストでできるようになるために、テスト予想問題を用意しました!
こちらの公式lineで解説を見ることができるので、チェックしてみてください!
これからも参考書のざっくりとした解説で困らないように丁寧に解説していきますので、チャンネル登録よろしくお願いします!
本日もご視聴ありがとうございました!


















コメント一覧