問の回答
(問) 回答
(1) 6
(2) 1/3(3分の1)
問 (1)の解説
(1) 直線①と直線②の交点のx座標が4であるとき、さいころBの出た目の数を求めなさい。の解説をしていきます。
まずは(ⅰ)、(ⅱ)の手順を行ってた時にXY座標でどのような直線になるのかを考えていきましょう。
(ⅰ)さいころAについて、偶数の目が出たらp=2、奇数の目が出たらp=-2とする。
pの値が変化することで、直線①の傾きが変化します。なぜなら直線①はy=px+qで、xの係数にpがあるからです。
まず「偶数の目が出たらP=2」の時の直線①を考えます。
このとき、直線①の式はy=2x+qとなり、グラフで見ると以下のようになります。qがy切片になることも確認しておきましょう。
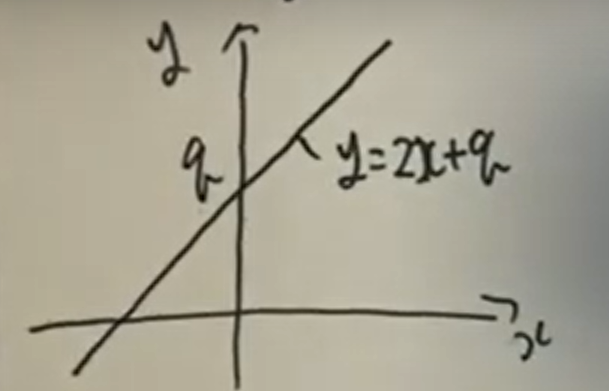
つぎに「奇数の目が出たらp=-2」の時の直線①を考えます。
このとき、直線①の式はy=-2x+qとなり、グラフで見ると以下のようになります。
これで、さいころAの目が偶数か奇数かによる直線①の形がわかりましたね。
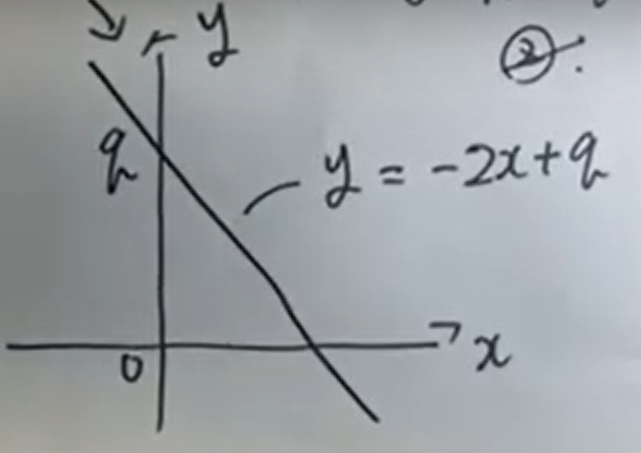
次に直線②について考えてみましょう
直線②の式はy=x-qでしたね。まずはこれをグラフに書いてみましょう。すると以下のようになります。
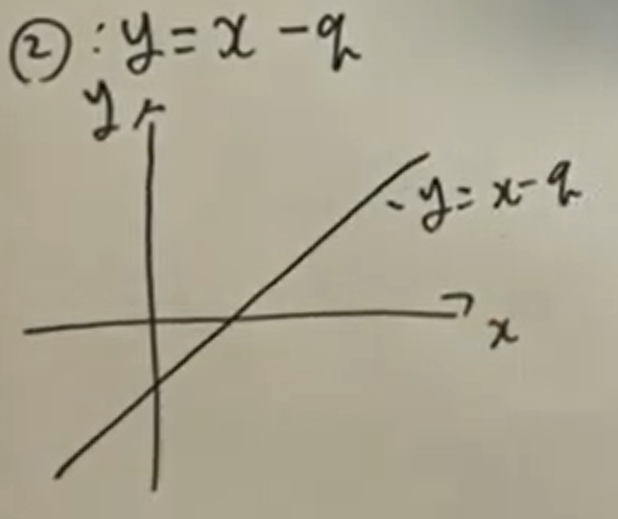
ここで(1)の問題をもう一度確認すると、「直線①と直線②の交点のx座標が4であるとき、さいころBの出た目の数を求めなさい。」となっています。
つまり、
さいころAが偶数の時の直線①y=2x+qと直線②y=x-qの交点のx座標が4となるとき、
さいころAが奇数の時の直線①y=-2x+qと直線②y=x-qの交点のx座標が4となるとき、
の二つの場合に分けて考える必要があります。
さいころAが偶数のときの直線①と直線②の交点を考える
さいころAが偶数の時の直線①y=2x+qと直線②y=x-qの交点のx座標が4となるとき、を考えてみましょう。
まずは直線①と直線②の交点のx座標を求めます。
一次関数で習ったことの復習になりますが、2つの直線の交点をもとめるときは、連立方程式を使いますよね。
y=2x+qとy=x-qを解くと、
2x+q=x-q
↓(xを左辺に、qを右辺に移項する)
x=-2q
つまりさいころAが偶数のときの直線①と直線②の交点のx座標は-2qとなります。
次に、この交点のx座標である-2qが4となるときを考えていきます。
つまり-2q=4となるときについて考えます。
ここで手順(ⅱ)を確認すると「さいころBの出た目の数をqとする。」と書いてありますね。
さいころの目は1~6しかないので、-2q=4が成立しないことがわかると思います。
よってさいころAが偶数の時は直線①と直線②の交点のx座標が4にならないことが分かりました。
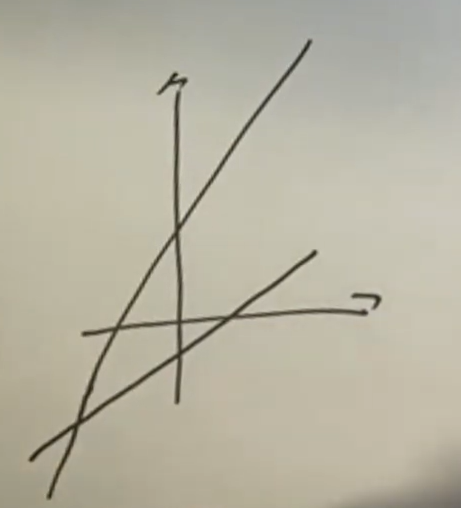
じっさいに、グラフを書いてみるとさいころAが偶数のときの直線①と直線②の交点のx座標は負になることがわかると思います。これは(2)の問題につながるので、覚えておいてください!
※上の直線がさいころAが偶数のときの直線①、下の直線が直線②
さいころAが奇数のときの直線①と直線②の交点を考える
次に、さいころAが奇数の時の直線①y=-2x+qと直線②y=x-qの交点のx座標が4となるとき、を考えてみましょう。
y=-2x+qとy=x-qの連立方程式を解くと
-2x+q=x-q
↓(xを左辺に、qを右辺に移項する)
-3x=-2q
↓(両辺に-1をかけて、符号を正にする)
3x=2q
↓(両辺を3で割る)
x=(2/3)q
つまりさいころAが奇数のときの直線①と直線②の交点のx座標は(2/3)qとなります。
次に、この交点のx座標である(2/3)qが4となるときを考えていきます。
つまり(2/3)q=4となるときについて考えます。
この式と解くと
(2/3)q=4
↓(両辺に3をかける)
2q=12
↓(両辺を2で割る)
q=6 ※もしくは(2/3)q=4の両辺を2/3で割る、または両辺に3/2をかけると答えが出る
qはさいころBの出た目の数なので、
(1) 直線①と直線②の交点のx座標が4であるとき、さいころBの出た目の数を求めなさい。
の答えは6となります。
問 (2)の解説
(2) 直線①と直線②の交点のx座標が-6以下である確率を求めなさい。の解説をしていきます。
まず、(1)で確認したように、直線①と直線②の交点のx座標が負になるのは、さいころAが偶数の時です。
もしこの時点でよくわからない場合は、(1)の解説をもう一度丁寧に読んでみてください。
なので、さいころAが偶数の時の直線①y=2x+qと直線②y=x-qの交点のx座標が-6以下になる場合を考えていきましょう。
(1)ではさいころAが偶数のときの直線①と直線②の交点のx座標は-2qとすでに求めているので、
この交点のx座標である-2qが-6以下となるときを考えていきます。
式は-2q≦-6となり、それを解いていくと
-2q≦-6
↓(両辺に-1をかけて、符号を正にする)※符号の向きが反対になるので注意
2q≧6
↓(両辺を2で割る)
q≧3
qはさいころBの出た目の数なので、さいころAの出た目が偶数のときで、かつ、さいころBの出た目が3以上のとき、直線①と直線②の交点のx座標は-6以下となることがわかりました。
最後に、この「さいころAが偶数のときで、かつ、さいころBの出た目が3以上のとき」の確率を求めます。
まず、さいころAの出た目が偶数になる確率について求めます。
さいころは6面あるので、全ての起こり得る場合は6通りとなります。
次にさいころの出た目が偶数となる場合は、2,4,6が出たときの3通りです。
つまり、さいころAが偶数になる確率は3/6、これを約分して1/2となります。
次にさいころBの出た目が3以上になる確率について求めます。
さいころは6面あるので、全ての起こり得る場合は6通りとなります。
つぎにさいころの出た目が3以上となる場合は、3,4,5,6が出たときの4通りです。
つまり、さいころBの出た目が3以上になる確率は4/6、これを約分して2/3となります。
「さいころAの出た目が偶数になる」という事象と、「さいころBの出た目が3以上になる」という事象は同時に起こるので、
「さいころAの出た目が偶数になる」確率と「さいころBの出た目が3以上になる」をかけることで、答えが出ます。
計算をすると、
(1/2)×(2/3)=1/3となります。
よって(2) 直線①と直線②の交点のx座標が-6以下である確率を求めなさい。
の答えは1/3となります。



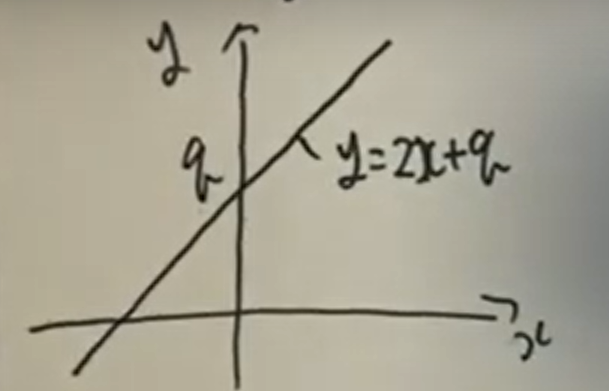
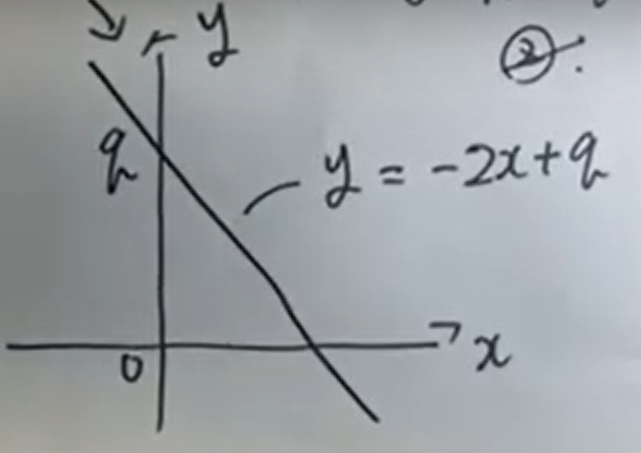

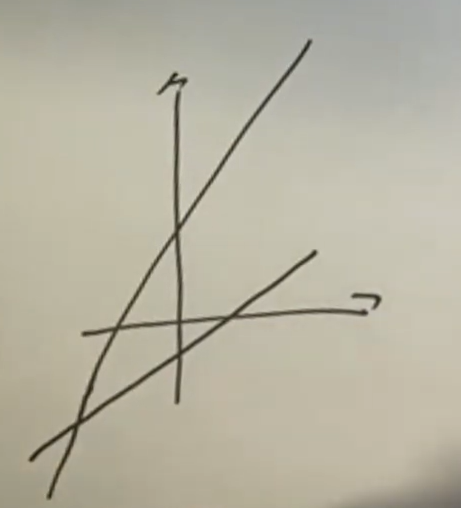











関連記事