【一次関数】一次関数のグラフの書き方 解説動画
本日は中2数学 一次関数のグラフの書き方についてやっていきたいと思います!
そもそもってなに?って思いますよね
しかも、参考書の解説がわかりづらくて勉強が嫌になるときありますよね
今回の動画では参考書ではありえないくらい丁寧に解説していきますので
高評価&チャンネル登録よろしくお願いします!
それでは本日の問題を見ていきましょう。
本日の問題はこちらになります。

解いてみたい方はここで一時停止をしてください。
では解いて行きましょう。
それでは、関数のグラフを書きたいということで本日のポイント①
グラフの書き方について説明してきたいと思います。
グラフの書き方は大きく分けて二つあります。
一つ目は一次関数のグラフが通る二点を探して結ぶだけという方法
二つ目が通る移転を探してから傾きを求めて直線を引いていく方法。
この二つになります。
それでは、それぞれの方法を使って今回の問題を解いていきましょう。

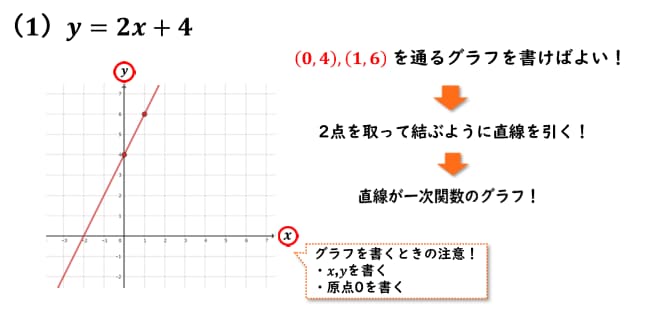
(1)y = 2x + 4 見ていきましょう。
こちらまず解法①、一次関数のグラフが通る二点を探して結ぶという方法で解いていってみましょう。
まずは切片で一点を取ってみましょう。
そうするとy = 2x + 4の切片は4なので、今回の一時関数は(0, 4)
の点を通るということが分かります。
それでは、もう一点を探していきましょう。
こちらは好きな点でOKです。
なので、y = 2x + 4にx = 1を代入してみましょう。
好きな点でおけとは言いましたが、xの値が5/2だったりとか50だったりすると計算がめんどくさくなるので、一番シンプ
ルなx = 1がお勧めです。
x = 2x + 4のxに1を代入してあげると、このようになり、
計算してあげるとのyの値は6であるということが分かりました。
よってxが1のとき、yが6なので(1, 6)の点を通るということが分かりました。
それでは、(0, 4), (1, 6)を通るグラフを書いてきましょう。
グラフを用意してあげると、このようになります。
そしてグラフを書く時の注意点なんですが、必ずxとyを書くようにしましょう。
そして、原点0を書いときましょうこちらを忘れると減点される可能性があるので気を付けましょう。
それでは、二点(0, 4), (1, 6)を通るグラフを書いていきましょう。グラフ上にこの二点を取るとこのようになります。
そして二点を結ぶように直線を引くとこのようになります。
この直線が一次関数のグラフとなります。
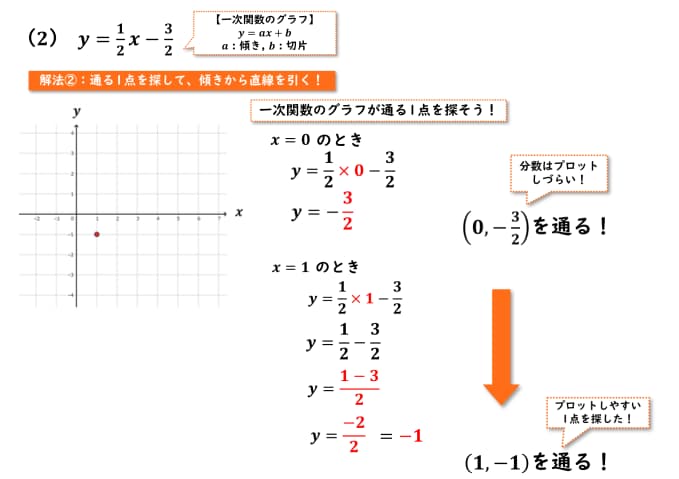
それでは次、(2)y = 1/2x – x – 2/3見ていきましょう。
それでは今回の問題、解法②、通る一点を探してから傾きから直線を求めていく方法で解いてみましょう。
ということで、一次関数のグラフが通る一点を探しましょう。
まずは、計算しやすいようにx = 0の時を考えていきましょう。x = 0をy = 1/2x – 2/3に代入してあげるとこのようにな
ります。計算をしてあげるとyの値は-3/2であるということが分かりました。
よって今回の一次関数(0, -3/2)を通るということが分かります。
ですが、分数はプロットしづらい、点を打ちにくいので、
x座標とy座標共に整数になるような値を見つけに行きましょう。
ということで、次はx = 1の時を考えましょう。
y = 1/2x – 3/2のxに1を代入してあげるとこのようになり、
計算をしてあげるとyの値は-1であるということが分かりました。
よって今回の一次関数は(1, -1)を通るということが分かりました。
なのでグラフ上に(1, -1)のところでプロットしてあげましょう。
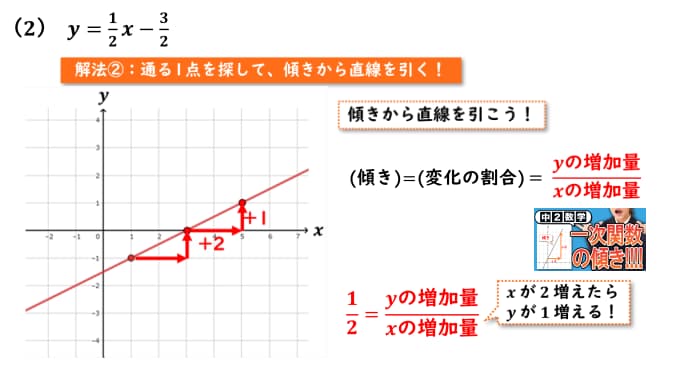
それでは傾きから直線を引いていこうということで、一次関数の傾きは変化の割合と等しかったです。
そして、変化の割合はxの増加量分のyの増加量であるということはもう習ったと思います。
傾きと変化の割合の関係について分からないよう忘れちゃったよ
という方は動画の概要欄の解説動画①をチェックしてみてください。
それでは本日の関数y = 1/2x – 3/2の傾きは1/2であるので、
この1/2が変化の割合と等しくxの増加量分のyの増加量であるということが分かります。
1/2 = xの増加量分のyの増加量なので、この意味はxが2増えたら、yが1増えるということになります。
よって先程プロットした(1, -1)からxを2増やしてあげてを1増やしてあげると
xの座標が3、yの座標が0を通るということが分かります。
なので、ここに二点目をプロットしてあげましょう。
そしてこの二点が結ばれるように直線を引いてあげれば、一次関数のグラフを求めることができます。
それでは、本日のポイント
二点を探して結ぶか、傾きを活用してもう一点を探してあげて直線を引くというやり方の二つになります。
そして、グラフを書く際の注意点が軸を書いたときは、
xとyの表記を書いてあげましょうということと、原点0をちゃんと書くようにしましょう。
本日の授業はいかがでしたでしょうか?
出来た出来ないなどコメントで教えてください。
数学の勉強について悩んでる人向けに公式Lineで質問に答えているので下のボタンから友達追加お願い致します。
Lafの公式LINEで分からない問題が簡単に質問できます!
問題を写真に撮ってチャットで質問できるので解き方が分からない問題があれば気軽に相談してね!
勉強を頑張っている皆さんが「テストでできる!」ようになるためにテスト予想問題を用意しました。

こちらも公式LINEで解説を見ることができるのでチェックしてみてください。
最後まで読んでいただきありがとうございました。

















コメント一覧