Laf創業・経営8年目【経歴/実績】
・これまで200名以上のお子様の指導実績あり
国公立をはじめとした難関高への進学をサポート
・AI先生をはじめとした日本初の教育サービスを展開
月間3,000人以上が利用するサービスへと育て上げる
AI先生を利用したことで模試C判定からA判定まで上がったと喜びの声も多数
利用者数3,000人突破！
動画解説AI先生
【平面図形】円の面積の問題 解説動画
本日は中1数学平面図形 円の面積の公式について解説していきます。
円の面積ってよくわからないと思う人も多いですよね。
参考書の解説もわかりづらくて勉強が嫌になることもあるのではないでしょうか。
今回は参考書ではありえないくらい丁寧に解説していきます。
前半で円の面積の公式について学習してから、練習問題に取り組んでみてください。
ちなみに、動画の最後にテスト予想問題を載せているのでチャレンジしてみてください！
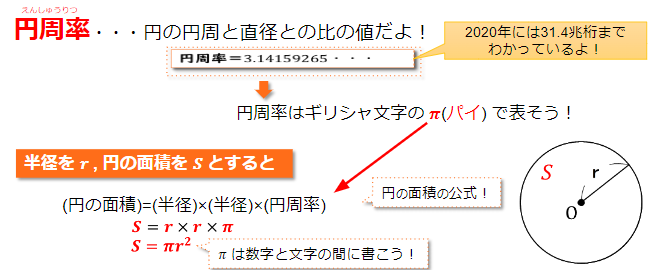
円の面積の公式について学習
円周率とは円の円周と直径との比の値のことをいいますよね。
そして円周率はギリシャ文字πを使って表すことができます。
半径をr、円の面積をSとする円があるとき、
S=πr²
という円の面積の公式が成り立ちます。
円の面積の公式 練習問題 問1
(1) 半径5cmの円の面積を求めよ。
(2) 円周の長さが40π cmである円の面積を求めよ。
円の面積の公式 練習問題 問1 回答と解説
問1の回答
(1) 25π cm²
(2) 400π cm²
問1 (1)の解説
円の面積の公式は「半径×半径×π」で式だとS=πr²とあわらすことができますよね。
今回半径が5cmなので式に代入すると、面積は25π cm²であるとわかります。
問1 (2)の解説
円の面積を求めるためには半径の長さが必要になるので、円周の長さから半径rを求めていきましょう。
円周を求める公式は円周をℓとしたとき、ℓ=2πrで求めることが出来ます。
今回の円周の長さは40π cmであることがわかるので、ℓ=2πrのlに40πを代入すると、
40π=2πr
↓
r=40 cm
これで、半径が40 cmであることが分かりました。
それでは半径rの値が求まったので、半径rから円の面積を求めていきましょう。
円の面積の公式はS=πr²でしたね。この式のrに20を代入すると、答えは400π cm²であると いうことが分かります。
円の面積の公式 練習問題 問2
(1) yをxの式で表しなさい。
(2) 半径が2倍になると、面積は何倍になりますか。
円の面積の公式 練習問題 問2 回答と解説
問2の回答
(問2) 回答
(1) y=πx²
(2) 4倍
問2 (1)の解説
円の面積の公式はS=πr²でしたね。
今回の問題では円の面積がy、半径がrなので
公式に代入するとy=πx²と表すことが出来ます。
問2 (2)の解説
半径がxのとき、円の面積はy=πx²となるのは(1)で確認しましたね。
では半径xが2倍の時、すなわち半径が2xの時の面積について計算してみましょう。
すると以下のように式を解くことが出来ます。
y=π(2x)²
↓
y=π(2x×2x)
↓
y=4πx²
よって半径が2xのとき、面積は4πx²となることが分かりました。
半径がxの時の面積πx²と比較すると、半径が2倍になると面積が4倍になったことが分かりました。
本日の授業はいかがでしたでしょうか。
コメント一覧